當前位置：試卷中心 > 試卷詳情

2023-2024學年湖南省長沙市周南中學高三（上）第二次段考數學試卷

發布：2024/8/21 16:0:1

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

1．已知集合M={x∈Z|x²-3x-4≤0}，N={x|0＜x≤3}，則M∩N=（　　）
A．{-1，0，1，2，3} B．{1，2，3} C．（0，3] D．[-1，4]
組卷：674引用：7難度：0.8
解析
2．已知復數z₁，z₂是方程x²-2x+5=0的兩個虛根，則|z₁-z₂|為（　　）
A．4 B．2 C．0 D．
5
組卷：30引用：2難度：0.7
解析
3．在△ABC中，M是AC邊上一點，且
AM
=
2
MC
，若
BM
=
x
BA
+
y
BC
，則y的值為（　　）
A．
-
1
3
B．
1
3
C．
-
2
3
D．
2
3
組卷：186引用：4難度：0.8
解析
4．若數列{a_n}滿足a₁=2，
a
n
+
1
=
1
+
a
n
1
-
a
n
，則a₂₀₂₄的值為（　　）
A．2 B．-3 C．
-
1
2
D．
1
3
組卷：223引用：4難度：0.8
解析
5．函數y=（x³-x）?3^|x|的圖象大致是（　　）
A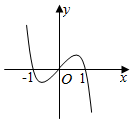． B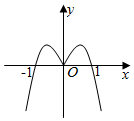． C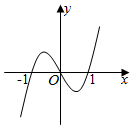． D．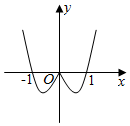
組卷：358引用：8難度：0.8
解析
6．已知菱形ABCD的邊長為2，∠BAD=60°，則將菱形ABCD以其中一條邊所在的直線為軸，旋轉一周所形成的幾何體的體積為（　　）
A．2π B．6π C．
4
3
π
D．8π
組卷：99引用：3難度：0.7
解析
7．已知
sin
（
α
-
π
6
）
+
cosα
=
3
5
，則
cos
（
2
α
+
π
3
）
=（　　）
A．
-
7
25
B．
7
25
C．
-
24
25
D．
24
25
組卷：1099引用：16難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

21．2020年1月15日教育部制定出臺了《關于在部分高校開展基礎學科招生改革試點工作的意見》（也稱“強基計劃”），《意見》宣布：2020年起不再組織開展高校自主招生工作，改為實行強基計劃，強基計劃主要選拔培養有志于服務國家重大戰略需求且綜合素質優秀或基礎學科拔尖的學生，據悉強基計劃的校考由試點高校自主命題，校考過程中通過筆試后才能進入面試環節．
（1）為了更好的服務于高三學生，某研究機構對隨機抽取的5名高三學生的記憶力x和判斷力y進行統計分析，得到如表數據．

x 6 8 9 10 12

y 2 3 4 5 6

請用相關系數說明該組數據中y與x之間的關系可用線性回歸模型進行擬合，并求y關于x的線性回歸方程
?
y
=
?
a
+
?
b
x.
（2）現有甲、乙兩所大學的筆試環節都設有三門考試科目且每門科目是否通過相互獨立，若某考生報考甲大學，每門筆試科目通過的概率均為
2
5
，該考生報考乙大學，每門筆試科目通過的概率依次為m,
1
4
，
2
3
，其中0＜m＜1，根據規定每名考生只能報考強基計劃的一所試點高校，若以筆試過程中通過科目數的數學期望為依據作出決策，求該考生更希望通過乙大學筆試時m的取值范圍．
參考公式：
①線性相關系數r=
n
∑
i
=
1
x
i
y
i
-
n
x
?
y
（
n
∑
i
=
1
x
i
2
-
n
x
2
）
（
n
∑
i
=
1
y
i
2
-
n
y
2
）
，一般地，相關系數r的絕對值在0.95以上（含0.95）認為線性相關性較強；否則，線性相關性較弱．
②對于一組數據（x₁，y₁），（x₂，y₂），…，（x_n，y_n），其回歸直線方程
?
y
=
?
b
x
+
?
a
的斜率和截距的最小二乘法估計公式分別為：
?
b
=
n
∑
i
=
1
x
i
y
i
-
n
x
?
y
n
∑
i
=
1
x
i
2
-
n
x
2
，
?
a
=
y
-
?
b
x
．
組卷：401引用：5難度：0.5
解析
22．已知函數f（x）=lnx-（m-1）x+1．
（1）若f（x）存在極值，求m的取值范圍；
（2）若m=0，已知方程
f
（
x
e
ax
）
=
2
有兩個不同的實根x₁，x₂，a∈R，證明：
x
1
+
x
2
＞
2
eln
1
a
．（其中e≈2.71828是自然對數的底數）
組卷：115引用：3難度：0.2
解析