已知a,b都是正數，ab為定值，求證：當a=b時，a+b有最小值2ab．
證明：∵a＞0，b＞0，
∴（a-b）2≥0，
∴a+b-2ab≥0，即a+b≥2ab，
∴當a=b時，有（a-b）2=0，
∴a+b=2ab，即a+b有最小值2ab．
請利用上述結論，解答下列問題：
（1）若a＞0，則當a=22時，a+4a取得最 小小值，為 44；
（2）若a＞1，求代數式a+25a-1的最小值；
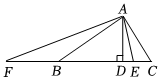
（3）如圖，在△ABC中，∠BAC=90°，AB=a,AC=b,點E在BC上，且BE=AB，點F在CB延長線上，且BF=AC．已知△ABC的面積為92，求線段EF的最小值．
ab
a
-
b
ab
ab
a
-
b
ab
ab
4
a
25
a
-
1
9
2
【答案】2；小；4
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/17 12:0:8組卷：104引用：1難度：0.5
相似題
-
1．在求解代數式2a2-12a+22的最值（最大值或最小值）時，老師給出以下解法：解：原式=2（a2-6a）+22=2（a2-6a+9）-18+22=2（a-3）2+4，∵無論a取何值，2（a-3）2≥0，∴代數式2（a-3）2+4≥4，即當a=3時，代數式2a2-12a+22有最小值為4．仿照上述思路，則代數式-3a2+6a-8的最值為（ ）
發布：2025/6/6 10:0:1組卷：472引用：3難度：0.7 -
2．若關于x的方程x2+2kx+k2+k+3=0有兩個實數根，則k2+k+3的最小值為 ．
發布：2025/6/6 8:0:1組卷：852引用：3難度：0.6 -
3．閱讀材料：若m2-2mn+2n2-8n+16=0，求m、n的值．
解：∵m2-2mn+2n2-8n+16=0，∴（m2-2mn+n2）+（n2-8n+16）=0
∴（m-n）2+（n-4）2=0，∴m-n=0，n-4=0，∴n=4，m=4．
根據你的觀察，探究下面的問題：
（1）已知x2+4xy+5y2+6y+9=0，求x-y的值．
（2）已知△ABC的三邊長a、b、c都是正整數，且滿足a2-4a+2b2-4b+6=0，求邊c的值．發布：2025/6/6 10:30:2組卷：582引用：6難度：0.6