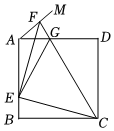
 如圖,正方形ABCD的邊長為2,點E在邊AB上運動(不與點A、B重合),∠DAM=45°,點F在射線AM上,且AF=2BE,CF與AD相交于點G,連接EC、EF、EG.則下列結論:①∠DCF+∠BCE=45°;②FC=2EF;③BE2+DG2=EG2;④△EAF面積的最大值為12;⑤△AEG的周長為(2+2),其中正確結論的序號為 ①,②,④①,②,④.
如圖,正方形ABCD的邊長為2,點E在邊AB上運動(不與點A、B重合),∠DAM=45°,點F在射線AM上,且AF=2BE,CF與AD相交于點G,連接EC、EF、EG.則下列結論:①∠DCF+∠BCE=45°;②FC=2EF;③BE2+DG2=EG2;④△EAF面積的最大值為12;⑤△AEG的周長為(2+2),其中正確結論的序號為 ①,②,④①,②,④.
AF
=
2
BE
FC
=
2
EF
1
2
(
2
+
2
)
【答案】①,②,④
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/12/5 20:30:4組卷:738引用:1難度:0.1
相似題
-
1.二次函數y=(x-3)2+1的最小值是( )
A.1 B.-1 C.3 D.-3 發布:2024/11/2 2:30:1組卷:549引用:7難度:0.9 -
2.y關于x的二次函數y=ax2+a2,在
時有最大值6,則a=.-1≤x≤12發布:2024/12/4 5:0:1組卷:1797引用:4難度:0.5 -
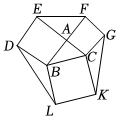 3.已知△ABC,AC=3,AB=4,以AB、AC、BC為邊向外作正方形ABDE、ACGF、BCKL,連接EF、DL、GK,則圖中以EF、DL、GK為邊的三個三角形面積和的最大值為( )
3.已知△ABC,AC=3,AB=4,以AB、AC、BC為邊向外作正方形ABDE、ACGF、BCKL,連接EF、DL、GK,則圖中以EF、DL、GK為邊的三個三角形面積和的最大值為( )A.6 B. 62C.18 D.6 3發布:2024/11/25 8:0:2組卷:47引用:1難度:0.5


