如圖，A、B、C三點均在邊長為1的小正方形網(wǎng)格的格點上．
（1）請在BC上標出點D，連接AD，使得△ABD∽△CBA；
（2）試證明上述結(jié)論：△ABD∽△CBA．
【考點】相似三角形的判定．
【答案】（1）見解析；
（2）證明過程見解析．
（2）證明過程見解析．
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/5/25 17:30:1組卷：1311引用：13難度：0.7
相似題
-
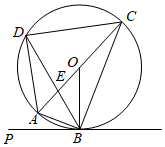1．如圖，四邊形ABCD內(nèi)接于⊙O，AC是⊙O的直徑，AC與BD交于點E，PB切⊙O于點B．
（1）求證：∠PBA=∠OBC；
（2）若∠PBA=20°，∠ACD=40°，求證：△OAB∽△CDE．發(fā)布：2025/5/25 23:0:2組卷：3660引用：12難度：0.5 -
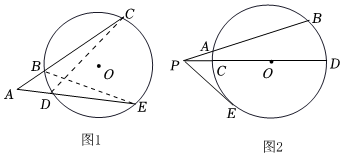2．閱讀與思考
請閱讀下列材料，并完成相應(yīng)的任務(wù)．
割線定理
是幾何中的一個基本定理，卻曾被民間數(shù)學家多次“發(fā)現(xiàn)”并“命名”割線定理是所示．點A是⊙O外一點，過點A作直線AC、AE分別交⊙O于點B，C，D，E，則有AB?AC=AD?AE．下面是割線定理的證明過程：
如圖1，連接BE和DC，∵∠BCD=∠BED（根據(jù)1），∠CAD=∠EAB，∴△ACD∽△AEB（根據(jù)2）∴∴AB?AC=AD?AE．ABAD=AEAC
任務(wù)：（1）材料中的根據(jù)1是指 ，根據(jù)2是指 ．
（2）如圖2，P為⊙O外一點，PB與⊙O交于點A、B，PD經(jīng)過圓心O，與⊙O交于點C、D，PE為⊙O的切線，切點為點E，若PA=，AB=35，⊙O的半徑為4，求切線PE的長．5發(fā)布：2025/5/25 23:0:2組卷：347引用：1難度：0.5 -
3．已知△ABC的一邊BC=5，另兩邊長分別是3，4，若P是△ABC邊BC上異于B，C的一點，過點P作直線截△ABC，截得的三角形與原△ABC相似，滿足這樣條件的直線有（ ）條．
發(fā)布：2025/5/25 17:30:1組卷：522引用：3難度：0.7
相關(guān)試卷