某店統計了近五年來創收利潤yi(單位:萬元)與時間ti(單位:年)的數據,列表如下:
| ti | 1 | 2 | 3 | 4 | 5 |
| yi | 2.4 | 2.7 | 4.1 | 6.4 | 7.9 |
附:相關系數公式:r=
n
∑
i
=
1
(
t
i
-
t
)
(
y
i
-
y
)
n
∑
i
=
1
(
t
i
-
t
)
2
n
∑
i
=
1
(
y
i
-
y
)
2
=
n
∑
i
=
1
t
i
y
i
-
n
t
y
n
∑
i
=
1
(
t
i
-
t
)
2
n
∑
i
=
1
(
y
i
-
y
)
2
參考數據:
56
.
95
5
∑
i
=
1
t
i
y
i
=
85
.
2
,
5
∑
i
=
1
(
t
i
-
t
)
2
=
10
,
5
∑
i
=
1
(
y
i
-
y
)
2
=
22
.
78
(2)專營店為吸引顧客,特推出兩種促銷方案.
方案一:每滿500元可減50元;
方案二:每滿500元可抽獎一次,每次中獎的概率都為
2
5
①某位顧客購買了1050元的產品、該顧客選擇參加兩次抽獎,求該顧客換得100元現金獎勵的概率.
②某位顧客購買了2000元的產品,作為專營店老板,是希望該顧客直接選擇返回200元現金,還是選擇參加四次抽獎?說明理由.
【答案】(1)r≈0.95,故y與他的線性相關程度很高,可以線性回歸方程擬合,理由詳見解析.(2)專營店老板希望顧客選擇參加四次抽獎,理由詳見解析.
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/27 10:35:59組卷:10引用:1難度:0.5
相似題
-
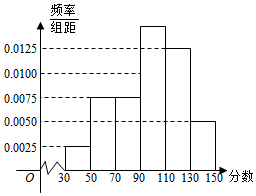 1.某市舉行“中學生詩詞大賽”,分初賽和復賽兩個階段進行,規定:初賽成績大于90分的具有復賽資格,某校有800名學生參加了初賽,所有學生的成績均在區間(30,150]內,其頻率分布直方圖如圖.
1.某市舉行“中學生詩詞大賽”,分初賽和復賽兩個階段進行,規定:初賽成績大于90分的具有復賽資格,某校有800名學生參加了初賽,所有學生的成績均在區間(30,150]內,其頻率分布直方圖如圖.
(Ⅰ)求獲得復賽資格的人數;
(Ⅱ)從初賽得分在區間(110,150]的參賽者中,利用分層抽樣的方法隨機抽取7人參加學校座談交流,那么從得分在區間(110,130]與(130,150]各抽取多少人?
(Ⅲ)從(Ⅱ)抽取的7人中,選出3人參加全市座談交流,設X表示得分在區間(130,150]中參加全市座談交流的人數,求X的分布列及數學期望E(X).發布:2024/12/29 13:30:1組卷:134引用:7難度:0.5 -
2.設離散型隨機變量X的分布列如表:
若離散型隨機變量Y=-3X+1,且E(X)=3,則( )X 1 2 3 4 5 P m 0.1 0.2 n 0.3 A.m=0.1 B.n=0.1 C.E(Y)=-8 D.D(Y)=-7.8 發布:2024/12/29 13:0:1組卷:199引用:6難度:0.5 -
3.從4名男生和2名女生中任選3人參加演講比賽,用X表示所選3人中女生的人數,則E(X)為( )
A.0 B.1 C.2 D.3 發布:2024/12/29 13:30:1組卷:139引用:6難度:0.7


