當(dāng)前位置：
2021-2022學(xué)年貴州省貴陽(yáng)市修文一中、華師一貴陽(yáng)學(xué)校聯(lián)考高二（下）期末數(shù)學(xué)試卷（理科）>
試題詳情
在平面直角坐標(biāo)系xOy中，曲線C1的參數(shù)方程為x=rcosα y=rsinα
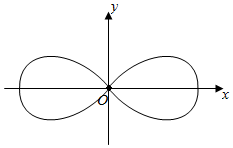
（0＜r＜2，α為參數(shù)），以O(shè)為極點(diǎn)，x軸的非負(fù)半軸為極軸建立極坐標(biāo)系，曲線C2：ρ2=4cos2θ（如圖所示）．
（1）若r=2，求曲線C1的極坐標(biāo)方程，并求曲線C1與C2交點(diǎn)的直角坐標(biāo)；
（2）已知曲線C2既關(guān)于原點(diǎn)對(duì)稱(chēng)，又關(guān)于坐標(biāo)軸對(duì)稱(chēng)，且曲線C1與C2交于不同的四點(diǎn)A，B，C，D，求矩形ABCD面積的最大值．
x = rcosα |
y = rsinα |
r
=
2
【考點(diǎn)】簡(jiǎn)單曲線的極坐標(biāo)方程；參數(shù)方程化成普通方程．
【答案】（1）（，），（，-），（-，），（-，-）；
（2）矩形ABCD面積的最大值為4．
6
2
2
2
6
2
2
2
6
2
2
2
6
2
2
2
（2）矩形ABCD面積的最大值為4．
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書(shū)面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：213引用：6難度：0.5
相似題
-
1．在直角坐標(biāo)系xOy中，以坐標(biāo)原點(diǎn)為極點(diǎn)，x軸正半軸為極軸建立極坐標(biāo)系，曲線C1：ρcosθ=3，曲線C2：ρ=4cosθ（
）．0≤θ＜π2
（1）求C1與C2交點(diǎn)的極坐標(biāo)；
（2）設(shè)點(diǎn)Q在C2上，，求動(dòng)點(diǎn)P的極坐標(biāo)方程．OQ=23QP發(fā)布：2024/12/29 3:0:1組卷：144引用：5難度：0.3 -
2．極坐標(biāo)方程ρcosθ=2sin2θ表示的曲線為（ ）
發(fā)布：2024/12/29 2:30:1組卷：244引用：6難度：0.7 -
3．已知點(diǎn)的極坐標(biāo)是
，則它的直角坐標(biāo)是（3，π4）．發(fā)布：2024/12/29 12:30:1組卷：12引用：2難度：0.7