定義：一組對角相等，另一組對角不相等的四邊形叫做“等對角四邊形”．
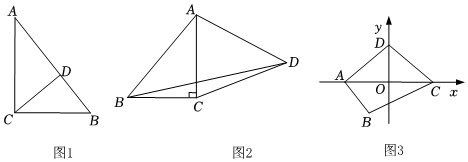
（1）如圖1，在Rt△ACB中，∠C=90°，AC=4，BC=3，CD平分∠ACB，點(diǎn)E在直線AC上，以點(diǎn)B、C、E、D為頂點(diǎn)構(gòu)成的四邊形為“等對角四邊形”，求AE的長．
（2）游山玩水是人們喜愛的一項(xiàng)戶外運(yùn)動(dòng)，但過度的旅游開發(fā)會(huì)對環(huán)境及動(dòng)植物的多樣性產(chǎn)生影響．如圖2，△ABC所在區(qū)域是某地著名的“黃花嶺”風(fēng)景區(qū)示意圖，點(diǎn)B位置是國家珍稀動(dòng)植物核心保護(hù)區(qū)，其中∠C=90°，BC=6km,AC=8km,該地旅游部門為科學(xué)合理開發(fā)此風(fēng)景區(qū)旅游資源，計(jì)劃在景區(qū)外圍D點(diǎn)建一個(gè)“嶺南山莊”度假村，據(jù)實(shí)際情況，規(guī)劃局要求：四邊形ABCD是一個(gè)“等對角四邊形”（∠BCD≠∠BAD），核心區(qū)B與山莊D之間要盡可能遠(yuǎn)，并且四邊形ABCD區(qū)域的面積要控制在56km2以內(nèi)．請問BD是否存在最大值，規(guī)劃局的要求能否實(shí)現(xiàn)？如果能，請求出BD的最大值及此時(shí)四邊形ABCD的面積；如果不能，請說明理由．
（3）如圖3，在平面直角坐標(biāo)系xOy中，四邊形ABCD是“等對角四邊形”，其中A（-2，0）、C（2，0）、B（-1，-3），點(diǎn)D在y軸上，拋物線過點(diǎn)A、C，點(diǎn)P在拋物線上，滿足∠APC=12∠ADC的點(diǎn)至少有3個(gè)時(shí)，總有不等式2n-94≤2c2+16a-82成立，直接寫出n的取值范圍．
3
1
2
9
4
2
【考點(diǎn)】二次函數(shù)綜合題．
【答案】（1）線段AE的長為1或或或25．
（2）BD最大值為+5，四邊形ABCD的面積=；
（3）n≤．
25
7
31
7
（2）BD最大值為
97
3492
+
180
97
97
（3）n≤
73
8
【解答】
【點(diǎn)評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/5/26 5:0:1組卷：171引用：1難度：0.1
相似題
-
1．如圖，在平面直角坐標(biāo)系中，已知A、B、C三點(diǎn)的坐標(biāo)分別為A（-2，0），B（6，0），C（0，3）．
（1）求經(jīng)過A、B、C三點(diǎn)的拋物線的解析式；
（2）過C點(diǎn)作CD平行于x軸交拋物線于點(diǎn)D，寫出D點(diǎn)的坐標(biāo)，并求AD、BC的交點(diǎn)E的坐標(biāo)；
（3）若拋物線的頂點(diǎn)為P，連接PC、PD，判斷四邊形CEDP的形狀，并說明理由．發(fā)布：2025/5/29 4:0:1組卷：252引用：21難度：0.1 -
2．如圖，AB、CD是半徑為1的⊙P兩條直徑，且∠CPB=120°，⊙M與PC、PB及弧CQB都相切，O、
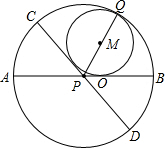Q分別為PB、弧CQB上的切點(diǎn)．
（1）試求⊙M的半徑r；
（2）以AB為x軸，OM為y軸（分別以O(shè)B、OM為正方向）建立直角坐標(biāo)系，
①設(shè)直線y=kx+m過點(diǎn)M、Q，求k,m；?????????????????
②設(shè)函數(shù)y=x2+bx+c的圖象經(jīng)過點(diǎn)Q、O，求此函數(shù)解析式；
③當(dāng)y=x2+bx+c＜0時(shí)，求x的取值范圍；
④若直線y=kx+m與拋物線y=x2+bx+c的另一個(gè)交點(diǎn)為E，求線段EQ的長度．發(fā)布：2025/5/29 5:0:1組卷：72引用：2難度：0.1 -
3．如圖，ABCD為平行四邊形，以BC為直徑的⊙O經(jīng)過點(diǎn)A，∠D=60°，BC=2，一動(dòng)點(diǎn)P在AD上移動(dòng)，過點(diǎn)P作直線AB的垂線，分別交直線AB、CD于E、F，設(shè)點(diǎn)O到EF的距離為t,若B、P、F三點(diǎn)能構(gòu)成三角形，設(shè)此時(shí)△BPF的面積為S．
（1）計(jì)算平行四邊形ABCD的面積；
（2）求S關(guān)于t的函數(shù)關(guān)系式，并寫出自變量t的取值范圍；
（3）△BPF的面積存在最大值嗎？若存在，請求出這個(gè)最大值，若不存在，請說明理由．發(fā)布：2025/5/29 5:30:2組卷：73引用：1難度：0.1