2021年江蘇省南通市中考數(shù)學第二次適應性訓練試卷

一．選擇題（共10小題，每題3分，共30分）

• 1．-5的絕對值的相反數(shù)是（　　）

  A．5

  B．-5

  C． 1 5

  D． - 1 5
  組卷：168引用：12難度：0.9

  解析

• 2．如圖，在Rt△ABC中，∠ACB=90°，CD⊥AB于點D，如果AC=3，AB=6，那么AD的值為（　　）

  A． 3 2

  B． 9 2

  C． 3 3 2

  D．3 3
  組卷：4413引用：32難度：0.9

  解析

• 3．小幸學習了在數(shù)軸上畫出表示無理數(shù)的點的方法后，進行以下練習：首先畫出數(shù)軸，原點為O，在數(shù)軸上找到表示數(shù)2的點A，然后過點A作AB⊥OA，使AB=3．以點O為圓心，OB為半徑作弧，交數(shù)軸正半軸于點P，則點P所表示的數(shù)介于（　　）

  A．3和3.5之間

  B．3.5和4之間

  C．4和4.5之間

  D．4.5和5之間
  組卷：239引用：5難度：0.8

  解析

• 4．如圖是一個幾何體的三視圖，根據(jù)圖中所示數(shù)據(jù)計算這個幾何體的表面積是（　　）

  A．20π

  B．18π

  C．16π

  D．14π
  組卷：2008引用：10難度：0.5

  解析

• 5．若一組數(shù)據(jù)1，2，3，4，x的平均數(shù)與中位數(shù)相同，則實數(shù)x的值不可能是（　　）

  A．0

  B．2.5

  C．3

  D．5
  組卷：3214引用：72難度：0.7

  解析

• 6．如圖，在Rt△ABC中，∠C=90°，AB=6，AD是∠BAC的平分線，經過A，D兩點的圓的圓心O恰好落在AB上，⊙O分別與AB、AC相交于點E、F．若圓半徑為2．則陰影部分面積（　　）

  A． 1 3 π

  B． 4 3 π

  C． 2 3 π

  D． 9 2 3 - 3
  組卷：1832引用：7難度：0.5

  解析

• 7．如圖，某大樓DE樓頂掛著“眾志成城，抗擊疫情”的大型宣傳牌，為了測量宣傳牌的高度CD，小江從樓底點E向前行走30米到達點A，在A處測得宣傳牌下端D的仰角為60°．小江再沿斜坡AB行走26米到達點B，在點B測得宣傳牌的上端C的仰角為43°，已知斜坡AB的坡度i=1：2.4，點A、B、C、D、E在同一平面內，CD⊥AE，宣傳牌CD的高度約為（參考數(shù)據(jù)：sin43°≈0.68，cos43°≈0.73，tan43°≈0.93，

  3

  ≈1.73）（　　）

  A．8.3米

  B．8.5米

  C．8.7米

  D．8.9米
  組卷：739引用：4難度：0.6

  解析

• 8．如圖，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，直線l經過點B，AE⊥l于點E，CF⊥l于點F，則AE+CF的最大值為（　　）

  A． 15 + 6

  B．5

  C．2 6 + 2

  D． 73
  組卷：173引用：2難度：0.6

  解析

• 9．如圖1，在菱形ABCD中，∠BAD=120°，點E是BC邊的中點，點P是對角線BD上一動點，設PD的長度為x,PE與PC的長度和為y,圖2是y關于x的函數(shù)圖象，其中H是圖象上的最低點，則a+b的值為（　　）
  

  A． 7 3

  B． 2 3 + 4

  C． 14 3 3

  D． 22 3 3
  組卷：2228引用：15難度：0.6

  解析

三．解答題（共11小題，共90分）

• 28．問題背景
  如圖（1），△ABD，△AEC都是等邊三角形，△ACD可以由△AEB通過旋轉變換得到，請寫出旋轉中心、旋轉方向及旋轉角的大小．
  嘗試應用
  如圖（2），在Rt△ABC中，∠ACB=90°，分別以AC，AB為邊，作等邊△ACD和等邊△ABE，連接ED，并延長交BC于點F，連接BD．若BD⊥BC，求

  DF

  DE

  的值．
  拓展創(chuàng)新
  如圖（3），在Rt△ABC中，∠ACB=90°，AB=2，將線段AC繞點A順時針旋轉90°得到線段AP，連接PB，直接寫出PB的最大值．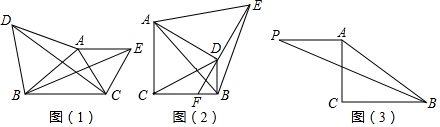
  
  組卷：4453引用：14難度：0.4

  解析

• 29．定義：一組對角相等，另一組對角不相等的四邊形叫做“等對角四邊形”．
  （1）如圖1，在Rt△ACB中，∠C=90°，AC=4，BC=3，CD平分∠ACB，點E在直線AC上，以點B、C、E、D為頂點構成的四邊形為“等對角四邊形”，求AE的長．
  （2）游山玩水是人們喜愛的一項戶外運動，但過度的旅游開發(fā)會對環(huán)境及動植物的多樣性產生影響．如圖2，△ABC所在區(qū)域是某地著名的“黃花嶺”風景區(qū)示意圖，點B位置是國家珍稀動植物核心保護區(qū)，其中∠C=90°，BC=6km,AC=8km,該地旅游部門為科學合理開發(fā)此風景區(qū)旅游資源，計劃在景區(qū)外圍D點建一個“嶺南山莊”度假村，據(jù)實際情況，規(guī)劃局要求：四邊形ABCD是一個“等對角四邊形”（∠BCD≠∠BAD），核心區(qū)B與山莊D之間要盡可能遠，并且四邊形ABCD區(qū)域的面積要控制在56km²以內．請問BD是否存在最大值，規(guī)劃局的要求能否實現(xiàn)？如果能，請求出BD的最大值及此時四邊形ABCD的面積；如果不能，請說明理由．
  （3）如圖3，在平面直角坐標系xOy中，四邊形ABCD是“等對角四邊形”，其中A（-2，0）、C（2，0）、B（-1，-

  3

  ），點D在y軸上，拋物線過點A、C，點P在拋物線上，滿足∠APC=

  1

  2

  ∠ADC的點至少有3個時，總有不等式2n-

  9

  4

  ≤2c²+16a-8

  2

  成立，直接寫出n的取值范圍．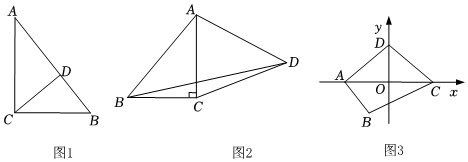
  
  組卷：171引用：1難度：0.1

  解析