閱讀理解:
材料1:對(duì)于一個(gè)關(guān)于x的二次三項(xiàng)式ax2+bx+c(a≠0),除了可以利用配方法求請(qǐng)多項(xiàng)式的取值范圍外,愛思考的小川同學(xué)還想到了其他的方法:比如先令ax2+bx+c=y(a≠0),然后移項(xiàng)可得:ax2+bx+(c-y)=0,再利用一元二次方程根的判別式來確定y的取值范圍,請(qǐng)仔細(xì)閱讀下面的例子:
例:求x2+2x+5的取值范圍.
解:令x2+2x+5=y,∴x2+2x+(5-y)=0,∴Δ=4-4×(5-y)≥0,∴y≥4,∴x2+2x+5≥4.
材料2:在學(xué)習(xí)完一元二次方程的解法后,愛思考的小川同學(xué)又想到仿造一元二次方程的解法來解決一元二次不等式的解集問題,他的具體做法如下:
若關(guān)于x的一元二次方程ax2+bx+c=0(a>0)有兩個(gè)不相等的實(shí)數(shù)根x1,x2(x1>x2),
則關(guān)于x的一元二次不等式ax2+bx+c≥0(a>0)的解集為:x≥x1或x≤x2.
則關(guān)于x的一元二次不等式ax2+bx+c≤0(a>0)的解集為:x2≤x≤x1.
請(qǐng)根據(jù)上述材料,解答下列問題:
(1)利用材料1,若關(guān)于x的二次三項(xiàng)式x2+ax+3(a為常數(shù))的最小值為-6,求a的值;
(2)利用材料2,若關(guān)于x的代數(shù)式5mx-nx2-x+2(其中m、n為常數(shù),且mn≠0)的最小值為-4,最大值為7,請(qǐng)求出滿足條件的m,n的值.
5
mx
-
n
x
2
-
x
+
2
【答案】(1)a=6或a=-6;
(2)
或
.
(2)
m = 14 5 |
n = 7 4 |
m = - 14 5 |
n = - 49 4 |
【解答】
【點(diǎn)評(píng)】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/9/17 13:0:8組卷:200引用:1難度:0.2
相似題
-
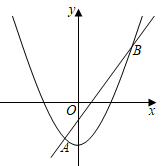 1.如圖.拋物線y=ax2+c與直線y=mx+n交于A(-1,p),B(3,q)兩點(diǎn),則不等式ax2+mx+c>n的解集為( )
1.如圖.拋物線y=ax2+c與直線y=mx+n交于A(-1,p),B(3,q)兩點(diǎn),則不等式ax2+mx+c>n的解集為( )A.x>-1 B.x<3 C.x<-3或x>1 D.-1<x<3 發(fā)布:2025/6/25 4:0:1組卷:485引用:7難度:0.6 -
 2.如圖,直線y=x+m和拋物線y=x2+bx+c都經(jīng)過點(diǎn)A(1,0),B(3,2).
2.如圖,直線y=x+m和拋物線y=x2+bx+c都經(jīng)過點(diǎn)A(1,0),B(3,2).
(1)求m的值和拋物線的解析式;
(2)求不等式x2+bx+c>x+m的解集.(直接寫出答案)發(fā)布:2025/7/1 13:0:6組卷:1342引用:64難度:0.5 -
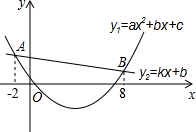 3.已知二次函數(shù)y1=ax2+bx+c(a≠0)與一次函數(shù)y2=kx+b(k≠0)的圖象相交于點(diǎn)A(-2,4),B(8,2),如圖所示,則能使y1<y2成立的x的取值范圍是 .發(fā)布:2025/6/24 16:30:1組卷:1361引用:49難度:0.7
3.已知二次函數(shù)y1=ax2+bx+c(a≠0)與一次函數(shù)y2=kx+b(k≠0)的圖象相交于點(diǎn)A(-2,4),B(8,2),如圖所示,則能使y1<y2成立的x的取值范圍是 .發(fā)布:2025/6/24 16:30:1組卷:1361引用:49難度:0.7


