閱讀并理解下面內容，解答問題．三角形的內心：定義：三角形的三條內角平分線相交于一點，這個點叫做三角形的內心．如圖1，已知AM，BN，CP是△ABC的三條內角平分線．求證：AM，BN，CP相交于一點．證明：如圖2，設AM，BN相交于點O，過點O分別作OD⊥BC，OE⊥AC，OF⊥AB，垂足分別為D，E，F．
∵點O是∠BAC的平分線AM上的一點，
∴OE=OF（依據1），
同理，OD=OF，
∴OD=OE（依據2）．
∵CP是∠ACB的平分線，
∴點O在CP上，（依據3）．
∴AM，BN，CP相交于一點．
請解答以下問題：
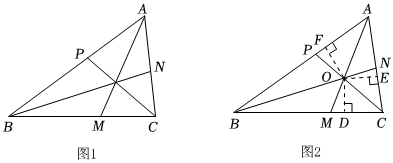
（1）上述證明過程中的“依據1”“依據2”“依據3”分別是指什么？
（2）如果BC=a,AC=b,AB=c,OD=r,請用a,b,c,r表示△ABC的面積．
【考點】角平分線的性質．
【答案】（1）依據1：角平分線上的點到角的兩邊的距離相等，
依據2：等量代換，
依據3：在角的內部，到角的兩邊的距離相等的點在這個角的平分線上；
（2）△ABC的面積為cr+br+ar．
依據2：等量代換，
依據3：在角的內部，到角的兩邊的距離相等的點在這個角的平分線上；
（2）△ABC的面積為
1
2
1
2
1
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/2 7:0:3組卷：394引用：3難度：0.6
相似題
-
1．如圖，在△ABC中，∠C=90°，∠A的平分線交BC于D，若S△ABD=20cm2，AB=10cm,則CD為cm.發布：2025/6/3 17:0:2組卷：635引用：6難度：0.5 -
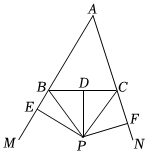2．如圖，P為△ABC外角∠CBM，∠BCN的平分線的交點，PD⊥BC，PE⊥AB，PF⊥AC，垂足分別為D，E，F．
（1）求證：PE=PF．
（2）若四邊形ABPC的面積為20，且PD=4，求AB+AC的長．發布：2025/6/3 22:30:1組卷：322引用：3難度：0.6 -
3．如圖，已知△ABC的周長是24，OB，OC分別平分∠ABC和∠ACB，OD⊥BC于D，且OD=4，△ABC的面積是 ．發布：2025/6/3 18:30:1組卷：166引用：4難度：0.6