綜合與實踐：
問題情境：
在綜合與實踐課上，數學老師出示了一道思考題：
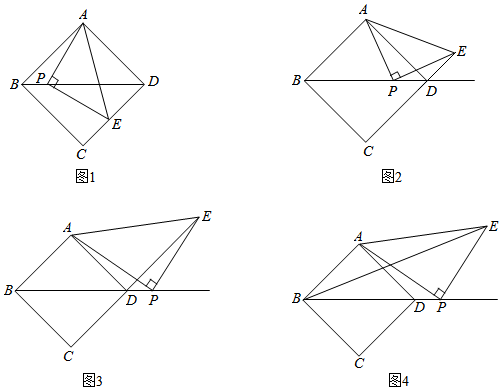
如圖，在正方形ABCD中，P是射線BD上一動點，以AP為直角邊在AP邊的右側作等腰直角三角形APE，使得∠APE=90°，AP=PE，且點E恰好在射線CD上．
獨立思考：
（1）如圖1，當點P在對角線BD上，點E在CD邊上時，那么BP與CE之間的數量關系是 BP=22CEBP=22CE；
探索發現：
（2）當點E在正方形ABCD外部時如圖2與圖3，（1）中的結論是否還成立？若成立，請利用圖2進行證明；若不成立，請說明理由；
問題解決：
（3）如圖4，在正方形ABCD中，AB=22，當P是對角線BD的延長線上一動點時，連接BE，若BE=62，求△BPE的面積．
2
2
2
2
2
2
【考點】四邊形綜合題．
【答案】BP=CE
2
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：560引用：3難度：0.1
相似題
-
1．在線上教學中，教師和學生都學習到了新知識，掌握了許多新技能．例如教材八年級下冊的數學活動一折紙，就引起了許多同學的興趣．在經歷圖形變換的過程中，進一步發展了同學們的空間觀念，積累了數學活動經驗．
實踐發現：
對折矩形紙片ABCD，使AD與BC重合，得到折痕EF，把紙片展平；再一次折疊紙片，使點A落在EF上的點N處，并使折痕經過點B，得到折痕BM，把紙片展平，連接AN，如圖①．
（1）①計算出∠MNE=°；
②繼續折疊紙片，使點A落在BC邊上的點H處，并使折痕經過點B，得到折痕BG，把紙片展平，如圖②，則∠GBN=°；
拓展延伸：
（2）如圖③，折疊矩形紙片ABCD，使點A落在BC邊上的點A'處，并且折痕交BC邊于點T，交AD邊于點S，把紙片展平，連接AA'交ST于點O，連接AT．求證：四邊形SATA'是菱形；
解決問題：
（3）如圖④，矩形紙片ABCD中，AB=10，AD=26，折疊紙片，使點A落在BC邊上的點A'處，并且折痕交AB邊于點T，交AD邊于點S，把紙片展平．同學們小組討論后，得出線段AT的長度有4，5，7，9．
請寫出以上4個數值中你認為正確的數值 ．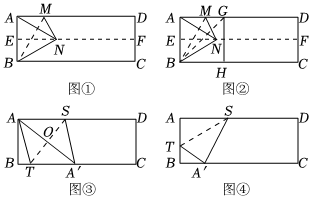
發布：2025/6/7 2:30:1組卷：127引用：1難度：0.3 -
2．已知正方形ABCD的邊長為4，△BEF為等邊三角形，點E在AB邊上，點F在AB邊的左側．
（1）如圖1，若D，E，F在同一直線上，求BF的長；
（2）如圖2，連接AF，CE，BD，并延長CE交AF于點H，若CH⊥AF，求證：AE+2FH=BD；2
（3）如圖3，將△ABF沿AB翻折得到△ABP，點Q為AP的中點，連接CQ，若點E在射線BA上運動時，請直接寫出線段CQ的最小值．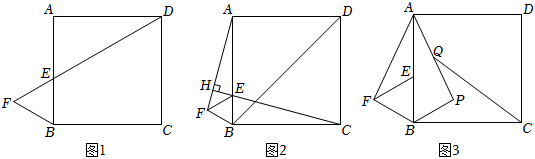
發布：2025/6/7 2:0:5組卷：1043引用：10難度：0.2 -
3．如圖1，在Rt△ABC中，∠ACB=90°，∠A=60°，CD平分∠ACB，試判斷BC和AC、AD之間的數量關系．
[探究]如圖2，在BC上取CA'=CA，連接DA'，得到一對全等三角形，從而將問題解決．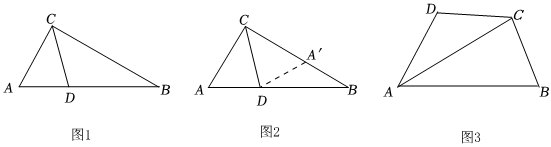
請回答下列問題：
（1）在圖2中，得到的哪對全等三角形？請證明；
（2）如圖2．試猜想BC和AC、AD之間的數量關系并證明；
（3）如圖3，在四邊形ABCD中，AC平分∠BAD，BC=CD=10，AC=17，AD=9，求AB的長．發布：2025/6/7 3:0:1組卷：219引用：1難度：0.4