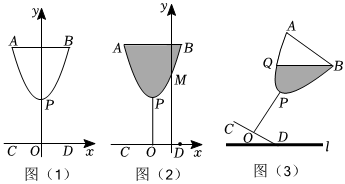
嘉琪家里有一款高腳杯，她發現高腳杯的杯體可以近似看成拋物線．于是她開始進行測量，并畫出了高腳杯的截面圖（杯體厚度忽略不計）如圖（1）．點P是拋物線的頂點，CD=OP=8cm.點O是CD的中點，且OP⊥CD，AB=12cm,杯子的高度（即CD，AB之間的距離）為20cm.嘉琪想借此考查一下對學過的知識掌握情況，于是以O為原點，CD所在直線為x軸，OP所在直線為y軸，建立平面直角坐標系（1個單位長度表示1cm），并提出了以下問題，你也來一起解決吧！
（1）求杯體APB所在拋物線的解析式；
（2）將杯子向左平移3cm,并倒滿飲料，杯體APB與y軸交于點M，如圖（2），過點A放一根吸管，吸管底部碰觸到杯壁后不再移動，喝過一次飲料后發現剩余飲料的液面低于點M，設吸管所在直線的解析式為y=kx+b,求k的取值范圍；
（3）將放在水平桌面l上的裝有飲料的高腳杯繞點D順時針旋轉30°，液面恰好到達點B處（BQ∥l），如圖（3）．
①請你以CD的中點O為原點，CD所在直線為x軸，OP所在直線為y軸，建立平面直角坐標系，并求出BQ與y軸的交點坐標；
②請直接寫出此時杯子內液體的最大深度．
【考點】二次函數綜合題．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/2 8:0:9組卷：598引用：4難度：0.1
相似題
-
1．平面直角坐標系xOy中，拋物線y=ax2-3ax+1與y軸交于點A．
（1）求點A的坐標及拋物線的對稱軸；
（2）當-1≤x≤2時，y的最大值為3，求a的值；
（3）已知點P（0，2），Q（a+1，1）．若線段PQ與拋物線只有一個公共點，結合函數圖象，求a的取值范圍．發布：2025/5/24 10:30:2組卷：1465引用：13難度：0.2 -
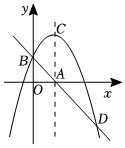2．如圖所示，在平面直角坐標系中，拋物線y=ax2+bx+c（a≠0）的頂點坐標為C（3，6），并與y軸交于點B（0，3），點A是對稱軸與x軸的交點，直線AB與拋物線的另一個交點為D．
（1）求拋物線的解析式；
（2）連接BC、CD，判斷△BCD是什么特殊三角形，并說明理由；
（3）在坐標軸上是否存在一點P，使△BDP為以BD為直角邊的直角三角形？若存在，直接寫出點P坐標；若不存在，說明理由．發布：2025/5/24 10:30:2組卷：294引用：1難度：0.1 -
3．如圖，在平面直角坐標系中，拋物線y=ax2+bx-3與x軸交于A（-1，0），B（3，0）兩點．
（1）求拋物線的解析式；
（2）已知點D（0，-1），點P為線段BC上一動點，連接DP并延長交拋物線于點H，連結BH，當四邊形ODHB的面積為時，求點H的坐標；112
（3）已知點E為x軸上一動點，點Q為第二象限拋物線上一動點，以CQ為斜邊作等腰直角三角形CEQ，請直接寫出點E的坐標．
發布：2025/5/24 10:30:2組卷：772引用：4難度：0.1