【問題情景】（1）如圖1，AB∥CD，∠PAB=135°，∠PCD=115°，求∠APC的度數(shù)；
【問題遷移】（2）如圖2，已知∠MON，AD∥BC，點P在射線OM上運動，當點P在A，B兩點之間運動時，連接PD，PC，∠ADP=∠α，∠BCP=∠β，求∠CPD與∠α，∠β之間的數(shù)量關(guān)系，并說明理由；
【知識拓展】（3）在（2）的條件下，若將“點P在A，B兩點之間運動”改為“點P在A，B兩點外側(cè)運動（點P與點A，B，O三點不重合）”其他條件不變，請直接寫出∠CPD與∠α，∠β之間的數(shù)量關(guān)系．
【考點】平行線的性質(zhì)．
【答案】見試題解答內(nèi)容
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/30 8:0:9組卷：190引用：4難度：0.5
相似題
-
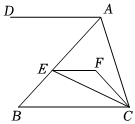1．如圖，EF∥AD，EF∥BC，∠DAC=115°，∠ACF=25°．
（1）求∠BCF的度數(shù)；
（2）若CE平分∠BCF，求∠FEC的度數(shù)．發(fā)布：2025/6/9 10:0:1組卷：141引用：3難度：0.5 -
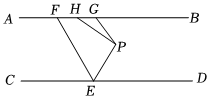2．如圖，點E、F分別為直線CD和AB上的點，點P為AB、CD之間一點，過點P作PG∥EF，交AB于點G，∠BGP=∠CEF，EF平分∠PEC，H為線段GF上一點，連接PH，若∠PHF+∠FEP=215°，則∠GPH=．發(fā)布：2025/6/9 10:0:1組卷：395引用：2難度：0.7 -
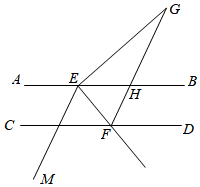3．如圖，點E、F分別在AB、CD上，AB∥CD，EG⊥EF于點E，F(xiàn)G平分∠EFD分別交AB、EG于點H、G．（解答過程請寫出每一步的依據(jù)）
（1）若∠G=25°，求∠GHB的度數(shù)；
（2）若EM平分∠AEF，證明：∠AEM=∠GHB．發(fā)布：2025/6/9 10:0:1組卷：595引用：3難度：0.7