2025年吉林省長春市朝陽區中考數學二模試卷

一、選擇題（每小題3分，共24分）

• 1．將函數y=2x-1的圖象以y軸為對稱軸翻折，所得到的函數解析式為（　　）

  A．y=2x+1

  B．y=-2x+1

  C．y=2x-1

  D．y=-2x-1
  組卷：1075引用：3難度：0.7

  解析

• 2．如圖，在△ABC中，AB=AC，AB+BC=8．將△ABC折疊，使得點A落在點B處，折痕DF分別與AB、AC交于點D、F，連接BF，則△BCF的周長是（　　）

  A．8

  B．16

  C．4

  D．10
  組卷：221引用：5難度：0.9

  解析

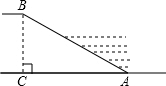• 3．河堤橫斷面如圖所示，堤高BC=6米，迎水坡AB的坡比為1：

  3

  ，則AB的長為（　　）

  A．12米

  B．4 3 米

  C．5 3 米

  D．6 3 米
  組卷：463引用：10難度：0.7

  解析

• 4．實數a,b在數軸上表示的位置如圖所示，則（　　）

  A．a＞b

  B．|a|＜|b|

  C．a+b＜0

  D．a-b＞0
  組卷：186引用：4難度：0.9

  解析

• 5．一個正多邊形每個內角都等于150°，若用這種多邊形拼接地板，需與下列選項中哪種正多邊形組合（　　）

  A．正三角形

  B．正四邊形

  C．正五邊形

  D．正六邊形
  組卷：323引用：3難度：0.8

  解析

• 6．如圖，過反比例函數

  y

  =

  9

  x

  （x＞0）的圖象上任意兩點A、B分別作x軸的垂線，垂足分別為C、D，連接OA、OB，設△AOC和△BOD的面積分別是S₁、S₂，比較它們的大小，可得（　　）

  A．S1＞S2	B．S1=S2
  C．S1＜S2	D．大小關系不能確定
  組卷：695引用：5難度：0.9

  解析

• 7．在△ABC中，BC=6，AC=3，過點C作CP⊥AB，垂足為P，則CP長的最大值為（　　）

  A．5

  B．4

  C．3

  D．2
  組卷：880引用：15難度：0.2

  解析

• 8．一個幾何體的三視圖如圖所示，那么這個幾何體是（　　）

  A．

  B．

  C．

  D．
  組卷：652引用：201難度：0.9

  解析

二、填空題（每小題3分，共18分）

• 9．長方體木箱的高是8，長比寬多5，體積是52，若設寬為x,則長為

  ，可列方程為

  ．
  組卷：88引用：1難度：0.5

  解析

• 10．已知5+

  7

  的小數部分為a,5-

  7

  的小數部分為b,則a+b=

   

  ．
  組卷：2403引用：7難度：0.5

  解析

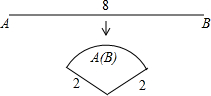• 11．如圖，將長為8cm的鐵絲首尾相接圍成半徑為2cm的扇形．則S_扇形=

  cm²．
  組卷：1619引用：76難度：0.9

  解析

• 12．已知a,b互為相反數，c,d互為倒數，x的絕對值是1，則代數式a+b+x²-cdx值可能是

  ．
  組卷：29引用：2難度：0.7

  解析

• 13．因式分解：a²-4a=

   

  ．
  組卷：796引用：38難度：0.7

  解析

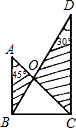• 14．將一副三角板按圖疊放，則△AOB與△DOC的面積之比等于

   

  ．
  組卷：7232引用：75難度：0.5

  解析

三、解答題（本大題10小題，共78分）

• 15．如圖1，拋物線y=ax²+bx（a≠0）經過點A（-4，0）及原點，且經過點B（4，8）．
  （1）求該拋物線的解析式；
  （2）連接OB，點P為x軸下方拋物線上一動點，過點P作OB的平行線交直線AB于點Q，當S_△POQ：S_△BOQ=1：2時，求出點P的坐標；
  （3）如圖2，若經過點D（-2，0）的直線與拋物線交于E、F兩點，點E在點F右邊，經過點K的兩直線KE、KF與拋物線均有唯一公共點，且KE、KF與y軸不平行，試說明點K在某條定直線上運動，并求出這條定直線．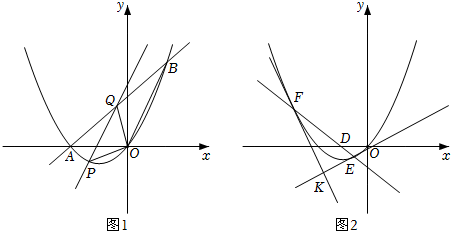
  
  組卷：735引用：2難度：0.2

  解析

• 16．把形狀、大小、質地完全相同的4張卡片分別標上數字-1、-4、0、2，將這4張卡片放入不透明的盒子中攪勻．求下列事件的概率：
  （1）從中隨機抽取一張卡片，卡片上的數字是負數；
  （2）先從盒子中隨機抽取一張卡片不放回，再隨機抽取一張，兩張卡片上的數字之積為0（用列表法或樹形圖）．
  組卷：251引用：64難度：0.5

  解析

• 17．已知Rt△ABC中，AC=BC=2．一直角的頂點P在AB上滑動，直角的兩邊分別交線段AC，BC于E．F兩點
  （1）如圖1，當

  AP

  PB

  =

  1

  3

  且PE⊥AC時，求證：

  PE

  PF

  =

  1

  3

  ；
  （2）如圖2，當

  AP

  PB

  =1時（1）的結論是否仍然成立？為什么？
  （3）在（2）的條件下，將直角∠EPF繞點P旋轉，設∠BPF=α（0°＜α＜90°）．連接EF，當△CEF的周長等于2+

  2

  3

  6

  時，請直接寫出α的度數．
  
  組卷：782引用：5難度：0.1

  解析

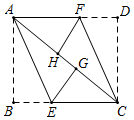• 18．【探究】在一次數學課上，老師出示了這樣一道題目：“如圖，在矩形ABCD中，AC：為對角線，AB＜AD，E、F分別為邊BC、AD上的點，連接AE、CF，分別將△ABE和△CDF沿AE、CF翻折，使點B、D的對稱點G、H都落在AC上，求證：四邊形AECF是平行四邊形．”以下是兩名學生的解題方法：
  甲學生的方法是：首先由矩形的性質和軸對稱的性質證得AB=CD，AD∥BC，∠AHF=90°，∠CGE=90°，易得AH=CG，可得△AFH≌△CEG（ASA），由平行四邊形的判定定理可得結論．
  乙學生的方法是：不利用三角形全等知識，依據平行四邊形的定義證明．
  （1）甲學生證明四邊形AECF是平行四邊形所用的判定定理的內容是

  ．
  （2）用乙學生的方法完成證明過程．
  【應用】當學生們完成證明后，老師又提出了一個問題：
  若四邊形AECF是菱形，則tan∠DAC的值為

  ．
  組卷：248引用：5難度：0.3

  解析

• 19．紅星中學課外興趣活動小組對某水稻品種的稻穗谷粒顆數進行調查，從試驗田中隨機抽取了30株，得到的數據如下：
  182，195，201，179，208，204，186，192，210，204，175，193，200，203，188
  197，212，207，185，206，188，186，198，202，221，199，219，208，187，224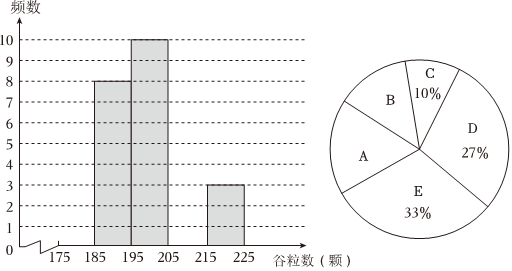
  
  （1）對抽取的30株水稻稻穗谷粒顆數進行統計分析，請補全下表，并完善頻數分布直方圖（如圖）；
  

  谷粒顆數x	頻數	對應扇形圖中區域
  175≤x＜185
  185≤x＜195	8	D
  195≤x＜205	10	E
  205≤x＜215
  215≤x＜225	3	C

  （2）在如圖所示的扇形統計圖中，扇形A對應的圓心角度數為

  °，扇形B對應的圓心角度數為

  °；
  （3）該試驗田中大約有3000株水稻，據此估計，其中稻穗谷粒顆數大于或等于205的水稻有多少株？
  組卷：21引用：4難度：0.5

  解析

• 20．甲、乙兩商場以同樣價格出售同樣的商品，并且又各自推出了不同的優惠方案：在甲商場累計購物超過200元后，超出200元的部分按80%收費；在乙商場累計購物超過100元后，超出100元的部分按90%收費．
  （1）當顧客累計購物不超過100元時，選擇到哪家商場購物花費少？（直接回答）
  （2）當顧客累計購物超過100元且不超過200元時，選擇到哪家商場購物花費少？（直接回答）
  （3）當顧客累計購物超過200元時，選擇到哪家商場購物花費少？請你運用所學的不等式知識計算回答．
  組卷：341引用：2難度：0.6

  解析

• 21．甲、乙兩個批發店銷售同一種蘋果，在甲批發店，不論一次購買數量是多少，價格均為6元/千克．在乙批發店，一次購買數量不超過50千克時，價格為7元/千克；一次購買數量超過50千克時，其中有50千克的價格仍為7元/千克，超過50千克部分的價格為5元/千克．設小王在同一個批發店一次購買蘋果的數量為x千克（x＞0）．
  （1）根據題意填表：
  

  一次購買數量/千克	30	50	150	…
  甲批發店花費/元	180			…
  乙批發店花費/元				…

  （2）設在甲批發店花費y₁元，在乙批發店花費y₂元，分別求y₁，y₂關于x的函數表達式．
  （3）根據題意填空：
  ①若小王在甲批發店和在乙批發店一次購買蘋果的數量相同，且花費相同，則他在同一個批發店一次購買蘋果的數量為

  千克；
  ②若小王在同一個批發店一次購買蘋果的數量為120千克，則他在甲、乙兩個批發店中的

  批發店購買花費少；
  ③若小王在同一個批發店一次購買蘋果花費了360元，則他在甲、乙兩個批發店中的

  批發店購買數量多．
  組卷：47引用：1難度：0.5

  解析

• 22．如圖，把兩張等寬的紙條交叉重疊在一起（不垂直）．
  
  （1）判斷圖1重疊部分四邊形ABCD的形狀，并說明理由．
  （2）如圖2，分別過B，D作BM⊥AD于M，作DN⊥BC于N，若BM=3，DM=4，求AM的長．
  組卷：280引用：1難度：0.5

  解析

• 23．計算：
  （1）|

  6

  -3|-（

  1

  3

  ）^-1+

  24

  
  （2）先化簡，再求值：（

  2

  a

  5

  a

  2

  b

  +

  3

  b

  10

  a

  b

  2

  ）÷

  7

  2

  a

  3

  b

  2

  ，其中a=

  5

  2

  ，b=-

  1

  2

  ．
  組卷：453引用：52難度：0.7

  解析

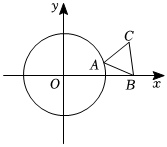• 24．如圖，⊙O的半徑為

  3

  ，正三角形ABC的頂點B的坐標為（2，0），頂點A在⊙O上運動．
  （1）當點A在x軸正半軸上時，求點C的坐標；
  （2）點A在運動過程中，是否存在直線AB與⊙O相切的位置關系？若存在，請直接寫出點C的坐標；
  （3）設點A的橫坐標為x,△ABC的面積為S，求S與x之間的函數關系式，并求出S的最大值與最小值．
  組卷：77引用：4難度：0.4

  解析