2018-2019學年北京四中九年級（下）開學數學試卷

一、選擇題（每小題2分，共16分）

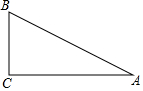• 1．如圖，在Rt△ABC中，∠C=90°，AC=4，tanA=

  1

  2

  ，則BC的長度為（　　）

  A．2

  B．8

  C． 4 3

  D． 4 5
  組卷：1028引用：21難度：0.9

  解析

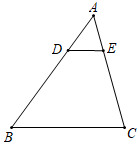• 2．如圖，D，E為△ABC的邊AB，AC上的點，DE∥BC，若AD：DB=1：3，DE=2，則BC的長是（　　）

  A．10

  B．8

  C．6

  D．4
  組卷：311引用：1難度：0.8

  解析

• 3．將二次函數y=x²-6x+5用配方法化成y=（x-h）²+k的形式，下列結果中正確的是（　　）

  A．y=（x-6）2+5

  B．y=（x-3）2+5

  C．y=（x-3）2-4

  D．y=（x+3）2-9
  組卷：3899引用：33難度：0.7

  解析

• 4．將拋物線y=-3x²平移，得到拋物線y=-3（x-1）²-2，下列平移方式中，正確的是（　　）

  A．先向左平移1個單位，再向上平移2個單位

  B．先向左平移1個單位，再向下平移2個單位

  C．先向右平移1個單位，再向上平移2個單位

  D．先向右平移1個單位，再向下平移2個單位
  組卷：3564引用：68難度：0.7

  解析

• 5．若點A（-2，y₁），B（1，y₂），C（3，y₃）在二次函數y=2x²+4x-1的圖象上，則y₁，y₂，y₃的大小關系是（　　）

  A．y1＜y2＜y3

  B．y2＜y3＜y1

  C．y3＜y2＜y1

  D．y2＜y1＜y3
  組卷：1041引用：5難度：0.6

  解析

• 6．若一個扇形的半徑是18cm,面積是54πcm²，則扇形的圓心角為（　　）

  A．30°

  B．60°

  C．90°

  D．120°
  組卷：513引用：2難度：0.7

  解析

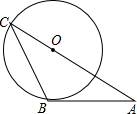• 7．如圖，AB是⊙O的切線，B為切點，AO的延長線交⊙O于C點，連接BC，若∠A=30°，AB=2

  3

  ，則AC等于（　　）

  A．4

  B．6

  C． 4 3

  D． 6 3
  組卷：994引用：15難度：0.9

  解析

• 8．二次函數y=ax²+bx+c（a,b,c為常數，且a≠0）中的x與y的部分對應值如表：
  

  x	…	-1	0	1	3	…
  y	…	-1	3	5	3	…

  下列結論：（1）ac＜0；（2）當x＞1時，y的值隨x值的增大而減小．（3）3是方程ax²+（b-1）x+c=0的一個根；（4）當-1＜x＜3時，ax²+（b-1）x+c＞0．其中正確的個數為（　　）

  A．1個

  B．2個

  C．3個

  D．4個
  組卷：1860引用：6難度：0.3

  解析

二、填空題（每小題2分，共16分）

• 9．若二次函數y=x²+2x+2k-4的圖象與x軸有兩個交點，則k的取值范圍為

  ．
  組卷：402引用：3難度：0.8

  解析

三、解答題

• 27．如圖1，在等腰直角△ABC中，∠ACB=90°，P是射線CB上一動點（與點C，B不重合），連接AP，延長BC至點Q，使得CQ=CP，過點作QH⊥AP于點H，交直線AB于點M．
  ①在圖1中補全圖形
  ②若∠PAC=α，用含α的式子表示∠AMQ的大小為∠AMQ=

  ；
  ③探究線段MB與PQ之間的數量關系，并給出證明．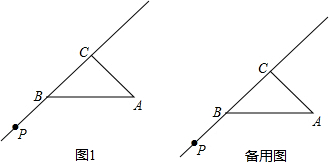
  
  組卷：100引用：1難度：0.5

  解析

• 28．在平面直角坐標系xOy中，⊙C的半徑為r,P是與圓心C不重合的點，點P關于⊙C的反稱點的定義如下：若在射線CP上存在一點P′，滿足CP+CP′=2r,則稱P′為點P關于⊙C的反稱點，如圖為點P及其關于⊙C的反稱點P′的示意圖．
  特別地，當點P′與圓心C重合時，規定CP′=0．
  （1）當⊙O的半徑為1時．
  ①分別判斷點M（2，1），N（

  3

  2

  ，0），T（1，

  3

  ）關于⊙O的反稱點是否存在？若存在，求其坐標；
  ②點P在直線y=-x+2上，若點P關于⊙O的反稱點P′存在，且點P′不在x軸上，求點P的橫坐標的取值范圍；
  （2）⊙C的圓心在x軸上，半徑為1，直線y=-

  3

  3

  x+2

  3

  與x軸、y軸分別交于點A，B，若線段AB上存在點P，使得點P關于⊙C的反稱點P′在⊙C的內部，求圓心C的橫坐標的取值范圍．
  組卷：3387引用：10難度：0.2

  解析