數(shù)學(xué)中，常對同一個量用兩種不同的方法計算，從而建立相等關(guān)系，我們把這一思想稱為“算兩次”．
[探究一]：
如圖1，在邊長為a的正方形紙片上剪去一個邊長為b（b＜a）的正方形，你能表示圖中陰影部分的面積嗎？陰影部分的面積是 a2-b2a2-b2．
如圖2，也可以把陰影部分沿著虛線AB剪開，分成兩個梯形，陰影部分的面積是 （a+b）（a-b）（a+b）（a-b）．
用兩種不同的方法計算同一個陰影部分的面積，可以得到等式 a2-b2=（a+b）（a-b）a2-b2=（a+b）（a-b）．
[探究二]：
如圖3，一條直線上有n個點，請你數(shù)一數(shù)共有多少條線段呢？
方法1：一路往右數(shù)，不回頭數(shù)．
以A1為端點的線段有A1A2、A1A3、A1A4、A1A5、…、A1An，共有（n-1）條；
以A2為端點的線段有A2A3、A2A4、A2A5、…、A2An，共有（n-2）條；
以A3為端點的線段有A3A4、A3A5、…、A3An，共有（n-3）條；
…
以An-1為端點的線段有An-1An，共有1條；圖中線段的總條數(shù)是 （n-1）+（n-2）+（n-3）+...+3+2+1（n-1）+（n-2）+（n-3）+...+3+2+1．
方法2：每一個點都能和除它以外的（n-1）個點形成線段，共有n個點，共可形成n（n-1）條線段，但所有線段都數(shù)了兩遍，所以線段的總條數(shù)是 n（n-1）2n（n-1）2．
用兩種不同的方法數(shù)線段，可以得到等式 （n-1）+（n-2）+（n-3）+?+3+2+1=n（n-1）2（n-1）+（n-2）+（n-3）+?+3+2+1=n（n-1）2．
[應(yīng)用]運用探究一、探究二中得到的等式解決問題．
計算：992-982+972-962+952-942+…+32-22+12．
n
（
n
-
1
）
2
n
（
n
-
1
）
2
（
n
-
1
）
+
（
n
-
2
）
+
（
n
-
3
）
+
?
+
3
+
2
+
1
=
n
（
n
-
1
）
2
（
n
-
1
）
+
（
n
-
2
）
+
（
n
-
3
）
+
?
+
3
+
2
+
1
=
n
（
n
-
1
）
2
【考點】平方差公式的幾何背景；列代數(shù)式．
【答案】a2-b2；（a+b）（a-b）；a2-b2=（a+b）（a-b）；（n-1）+（n-2）+（n-3）+...+3+2+1；；
n
（
n
-
1
）
2
（
n
-
1
）
+
（
n
-
2
）
+
（
n
-
3
）
+
?
+
3
+
2
+
1
=
n
（
n
-
1
）
2
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：156引用：1難度：0.5
相似題
-
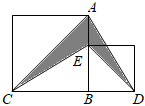1．如圖，大正方形與小正方形的面積之差是80，則陰影部分的面積是（ ）發(fā)布：2024/12/23 20:0:2組卷：845引用：5難度：0.7 -
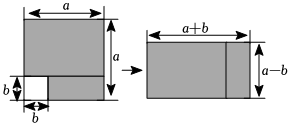2．如圖，從邊長為a的大正方形紙板的邊上挖去一個邊長為b的小正方形紙板后，沿著小正方形的缺口，將其裁成兩個長方形，然后拼成一個長方形．那么通過計算兩個圖形陰影部分的面積，可以驗證成立的公式為（ ）發(fā)布：2024/12/23 8:30:2組卷：234引用：4難度：0.8 -
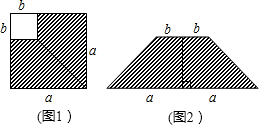3．如圖1，在邊長為a的正方形中剪去一個邊長為b的小正方形（a＞b），把剩下部分拼成一個梯形（如圖2），利用這兩幅圖形面積，可以驗證的公式是（ ）發(fā)布：2024/12/23 8:30:2組卷：5245引用：46難度：0.9