如圖，C為線段BD上一動點，分別過點B、D作AB⊥BD，ED⊥BD，連接AC、EC．已知AB=5，D
E=2，BD=12，設CD=x.
（1）用含x的代數式表示AC+CE的長；
（2）請問點C在BD上什么位置時，AC+CE的值最小？
（3）根據（2）中的規(guī)律和結論，請構圖求出代數式x2+9+（24-x）2+16的最小值．
x
2
+
9
+
（
24
-
x
）
2
+
16
【考點】軸對稱-最短路線問題．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網所有，未經書面同意，不得復制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：1038引用：7難度：0.1
相似題
-
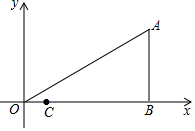1．如圖，在平面直角坐標系中，已知Rt△ABO的頂點B在x軸正半軸上，∠AOB=30°，OA=2，C（3，0），P為OA上的一個動點，12
（1）求點A的坐標；
（2）求PB+PC的最小值．發(fā)布：2025/6/23 16:30:1組卷：56引用：1難度：0.3 -
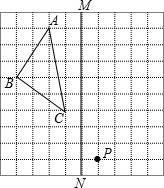2．如圖，在正方形網格上的一個△ABC．（其中點A、B、C均在網格上）
（1）作△ABC關于直線MN的軸對稱圖形△A′B′C′；
（2）以P點為一個頂點作一個與△ABC全等的△EPF（規(guī)定點P與點B對應，另兩頂點都在圖中網格交點處）．
（3）在MN上畫出點Q，使得QA+QC最小．發(fā)布：2025/6/23 19:30:1組卷：229引用：3難度：0.5 -
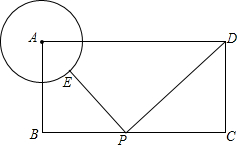3．如圖，矩形ABCD中，AB=2，BC=3，以A為圓心，1為半徑畫⊙A，E是圓⊙A上一動點，P是BC上一動點，則PE+PD最小值是（ ）發(fā)布：2025/6/23 18:0:2組卷：1138引用：18難度：0.9