在平面上畫互相垂直的兩組平行線，相鄰平行線的距離都等于1，這兩組平行線的交點稱為“格點”，以格點為頂點的三角形稱為“格點三角形”，如圖1．關于格點三角形的面積S，有一個著名的Pick定理：S=I+12B-1，其中I，B分別表示三角形內部與周界上的格點數．
（1）閱讀
我們把互相垂直的其中兩對平行線圍成的矩形稱為“格點矩形”，如圖2，可驗證Pick定理對格點矩形成立．設矩形ABCD的邊AB，AD上分別有m,n個格點（不包括端點），并記矩形內部和周界上的格點數分別為I0，B0，則I0=mn,B0=2（m+n）+4，AB=m+1，AD=n+1.I0+12B0-1=mn+12[2（m+n）+4]-1=mn+m+n+1=（m+1）（n+1） =SABCD.
完成下列兩題的證明
（2）任何一個格點三角形都可以內接在一個格點矩形中，使三角形至少有一個頂點恰好是矩形的頂點．
圖3是最簡單的情形．設邊AC上的格點數為k（不包括端點），請用I0，B0和k分別表示△ABC內部和周界上的格點數，并利用（1）的結論證明：對于△ABC，Pick定理成立．
（3）請利用（2）的結論證明：對于圖4所示的△ABC，Pick定理也成立．
S
=
I
+
1
2
B
-
1
I 0 + 1 2 B 0 - 1 = mn + 1 2 [ 2 （ m + n ） + 4 ] - 1 = mn + m + n + 1 = （ m + 1 ） （ n + 1 ） |
= S ABCD . |
【考點】四邊形綜合題．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：37引用：1難度：0.5
相似題
-
1．（1）問題發現：如圖①，正方形AEFG的兩邊分別在正方形ABCD的邊AB和AD上，連接CF．
①寫出線段CF與DG的數量關系 ；
②寫出直線CF與DG所夾銳角的度數 ．
（2）拓展探究：
如圖②，將正方形AEFG繞點A逆時針旋轉，在旋轉的過程中，（1）中的結論是否仍然成立？請利用圖②進行說明．
（3）問題解決
如圖③，△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，AB=AC=4，O為AC的中點．點D在直線BC上運動，連接OE，則在點D的運動過程中，求線段OE的長的最小值．（直接寫出結果）
發布：2025/6/2 23:30:2組卷：143引用：1難度：0.1 -
2．（1）發現；如圖1，在等腰直角三角形ABC中，∠ACB=90°，點F為BC上一點，以BF為邊作正方形BFED，點E在AB上，若AC=BC=2，
，則BF=2=；AECF
（2）探究：如圖2，在（1）的條件下，將正方形BFED繞點B旋轉，連接AE，CF，求的值；AECF
（3）拓展：在（2）的條件下，當A，E，F三點共線時候，直接寫出線段CF的長．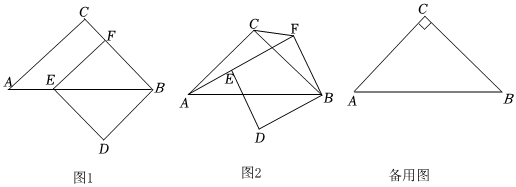
發布：2025/6/2 23:30:2組卷：29引用：1難度：0.2 -
3．探究：如圖1和圖2，四邊形ABCD中，已知AB=BC，∠ABC=90°，點M、N分別在CD、AD上，∠1=45°．
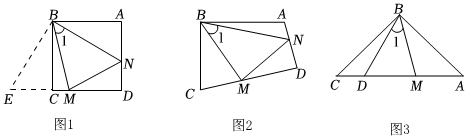
（1）①如圖1，若∠A、∠C都是直角，把△BAN繞點B順時針旋轉90°至△BCE，使AB與BC重合，直接寫出線段AN、CM和MN之間的數量關系 ；
②如圖2，若∠A、∠C都不是直角，但滿足∠A+∠C=180°，線段AN、CM和MN之間的結論是否仍然成立，若成立，請寫出證明過程，若不成立，請說明理由；
（2）拓展：如圖3，在△ABC中，∠CBA=90°，BC=BA=3，點D、M均在邊AC邊上，且∠1=45°，若CD=2，請直接寫出DM的長．2發布：2025/6/2 23:0:2組卷：281引用：1難度：0.2