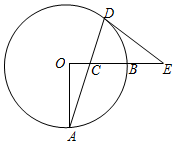
古希臘數學家畢達哥拉斯認為：“一切平面圖形中最美的是圓”．波波決定研究一下圓．如圖，OA、OB是⊙O的兩條半徑，OA⊥OB，C是半徑OB上一動點，連接AC并延長交⊙O于D，過點D作圓的切線交OB的延長線于E，已知OA=6．
（1）求證：∠ECD=∠EDC；
（2）若BC=2OC，求DE長；
（3）當∠A從15°增大到30°的過程中，求弦AD在圓內掃過的面積．
【答案】（1）證明過程見解析；
（2）8；
（3）3π+9-9．
（2）8；
（3）3π+9
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/26 7:0:1組卷：363引用：2難度：0.6
相似題
-
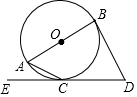1．如圖，AB是圓O的直徑，DB，DC分別切圓O于點B，C，若∠ACE=25°，則∠D的度數是（ ）發布：2025/1/28 8:0:2組卷：147引用：2難度：0.7 -
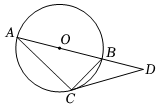2．如圖，AB為圓O的直徑，直線CD為圓O的切線，且BC=BD，若AB=6，則CD的長度為（ ）發布：2025/1/28 8:0:2組卷：548引用：1難度：0.6 -
3．如圖，AB是圓O的直徑，BC是⊙O的切線，點D，E是⊙O上的點，連接BD，DE，AE，延長AE交BC于點C．
（1）求證：∠BDE=∠CBE；
（2）若BD平分∠ABE，延長BA，ED交于點F，AF=OB，DF=4，求DE的長．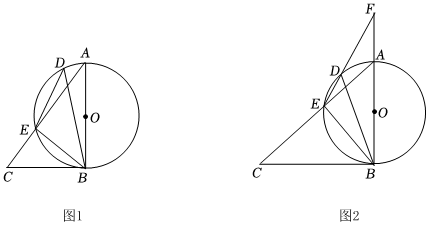
發布：2025/1/28 8:0:2組卷：172引用：1難度：0.5