 數學課外活動小組的同學在學習了完全平方公式之后,針對兩個正數之和與這兩個正數之積的算術平方根的兩倍之間的關系進行了探究,請閱讀以下探究過程并解決問題.
數學課外活動小組的同學在學習了完全平方公式之后,針對兩個正數之和與這兩個正數之積的算術平方根的兩倍之間的關系進行了探究,請閱讀以下探究過程并解決問題.
猜想發現
由5+5=25×5=10;13+13=213×13=23;0.4+0.4=20.4×0.4=0.8;15+5>215×5=2;0.2+3.2>20.2×3.2=1.6;12+18>212×18=12.
猜想:如果a>0,b>0,那么存在a+b≥2ab(當且僅當a=b時等號成立).
猜想證明
∵(a-b)2≥0,
∴①當且僅當a-b=0,即a=b時,a-2ab+b=0,∴a+b=2ab;
②當a-b≠0,即a≠b時,a-2ab+b>0,∴a+b>2ab.
綜合上述可得:若a>0,b>0,則a+b≥2ab成立(當且僅當a=b時等號成立).
猜想運用
對于函數y=x+1x(x>0),當x取何值時,函數y的值最小?最小值是多少?
變式探究
對于函數y=1x-3+x(x>3),當x取何值時,函數y的值最小?最小值是多少?
拓展應用
疫情期間,為了解決疑似人員的臨時隔離問題.高速公路檢測站入口處,檢測人員利用檢測站的一面墻(墻的長度不限),用63米長的鋼絲網圍成了9間相同的長方形隔離房,如圖.設每間隔離房的面積為S(米2).問:每間隔離房的長、寬各為多少時,可使每間隔離房的面積S最大?最大面積是多少?
5
×
5
1
3
1
3
1
3
×
1
3
2
3
0
.
4
×
0
.
4
1
5
1
5
×
5
0
.
2
×
3
.
2
1
2
1
8
1
2
×
1
8
=
1
2
ab
a
b
a
b
ab
ab
a
b
ab
ab
ab
1
x
1
x
-
3
【考點】反比例函數綜合題.
【答案】猜想運用:x=1時,函數y的最小值為2;變式探究:x=4時,函數y的最小值為5;拓展應用:每間隔離房長為米,寬為米時,S的最大值為.
7
2
21
8
147
16
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/7/21 8:0:9組卷:971引用:5難度:0.5
相似題
-
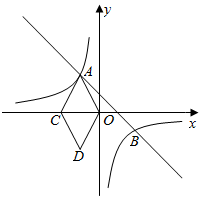 1.如圖,一次函數y=mx+1的圖象與反比例函數y=的圖象相交于A、B兩點,點C在x軸負半軸上,點D(-1,-2),連接OA、OD、DC、AC,四邊形OACD為菱形.kx
1.如圖,一次函數y=mx+1的圖象與反比例函數y=的圖象相交于A、B兩點,點C在x軸負半軸上,點D(-1,-2),連接OA、OD、DC、AC,四邊形OACD為菱形.kx
(1)求一次函數與反比例函數的解析式;
(2)根據圖象,直接寫出反比例函數的值小于2時,x的取值范圍;
(3)設點P是直線AB上一動點,且S△OAP=S菱形OACD,求點P的坐標.12發布:2025/5/25 4:30:1組卷:1258引用:5難度:0.5 -
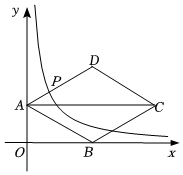 2.如圖,菱形ABCD在第一象限,點A、B分別在y軸、x軸上,對角線AC∥x軸,點C(12,3),反比例函數y=(x>0)的圖象交邊AD于點P,且AP:PD=1:2.kx
2.如圖,菱形ABCD在第一象限,點A、B分別在y軸、x軸上,對角線AC∥x軸,點C(12,3),反比例函數y=(x>0)的圖象交邊AD于點P,且AP:PD=1:2.kx
(1)求k的值.
(2)將菱形ABCD沿y軸向下平移m個單位,當點D落在反比例函數y=(x>0)的圖象時,求菱形ABCD平移所掃過的面積.kx發布:2025/5/25 8:30:2組卷:93引用:1難度:0.4 -
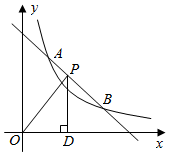 3.如圖,一次函數y1=-x+4與反比例函數y2=(x>0)的圖象交于A,B兩點.3x
3.如圖,一次函數y1=-x+4與反比例函數y2=(x>0)的圖象交于A,B兩點.3x
(1)求點A,點B的坐標:
(2)點P是直線AB上一點,設點P的橫坐標為m.填空:
①當y1<y2時,m的取值范圍是;
②點P在線段AB上,過點P作PD⊥x軸于點D,連接OP.若△POD的面積最小時,則m的值為.發布:2025/5/25 5:30:2組卷:510引用:10難度:0.6


