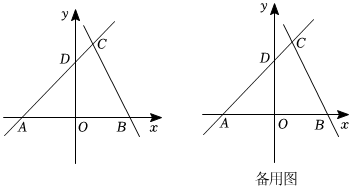
如圖，在平面直角坐標系中，點A，B均在x軸上，點C在第一象限，直線AC與y軸交于點D，且直線AC上所有點的坐標（x,y）都是二元一次方程x-y=-3的解，直線BC上所有點的坐標（x,y）都是二元一次方程2x+y=6的解．
（1）求點C的坐標時，小聰是這樣想的：先設點C的坐標為（m,n），因為點C在直線AC上，所以（m,n）是方程x-y=-3的解；又因為點C在直線BC上，所以（m,n）是方程2x+y=6的解，從而m,n滿足m-n=-3 2m+n=6
，據此可求出點C的坐標為 （1，4）（1，4），再求出點A的坐標為 （-3，0）（-3，0），點B的坐標為 （3，0）（3，0）．
（2）求四邊形BODC的面積；
（3）點E（x,y）是線段BC上一點，若點E的縱坐標y＞2，則點E的橫坐標x的取值范圍是 1≤x＜21≤x＜2；
（4）在y軸上是否存在點P，使三角形ACP的面積等于三角形ABC面積的23倍？若存在，請求出點P的坐標；若不存在，請說明理由．
m - n = - 3 |
2 m + n = 6 |
2
3
【考點】四邊形綜合題．
【答案】（1，4）；（-3，0）；（3，0）；1≤x＜2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/20 8:0:9組卷：135引用：1難度：0.3
相似題
-
1．如圖，∠MON=90°，四邊形ABCD是正方形，且點A、D始終分別在射線OM和ON上．
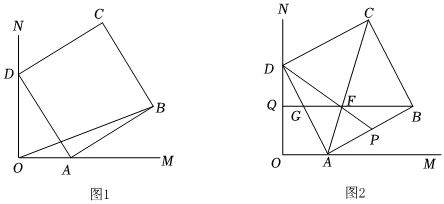
（1）如圖1，若AB=4，點A、D在OM，ON上滑動過程中，OB何時取最大值，并求出此最大值．
（2）如圖2，點P在AB上，且∠PDA=∠ODA，DP交AC于點F，延長射線BF交AD，ON分別于點G、Q．
①求證：BQ⊥ON．
②若OD=，求△DFQ的周長．6發布：2025/6/9 5:0:1組卷：50引用：2難度：0.1 -
2．下面是小明復習全等三角形時遇到的一個問題并引發的思考，請幫助小明完成以下學習任務．
如圖，OC平分∠AOB，點P在OC上，M、N分別是OA、OB上的點，OM=ON，求證：PM=PN．
小明的思考：要證明PM=PN，只需證明△POM≌△PON即可．
證法：如圖1，∵OC平分∠AOB，∴∠AOC=∠BOC，
又∵OP=OP，OM=ON，∴△MOP≌△NOP，
∴PM=PN；
請仔細閱讀并完成以下任務：
（1）小明得出△MOP≌△NOP的依據是 （填序號）．
①SSS，②SAS，③AAS，④ASA，⑤HL．
（2）如圖②，在四邊形ABCD中，AB=AD+BC，∠DAB的平分線和∠ABC的平分線交于CD邊上點P，求證：PC=PD．
（3）在（2）的條件下，如圖③，若AB=10，tan∠PAB=，當△PBC有一個內角是45°時，△PAD的面積是 ．12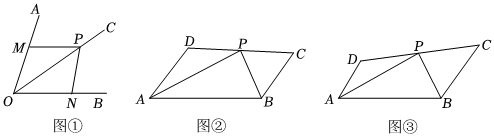
發布：2025/6/9 3:30:1組卷：114引用：3難度：0.3 -
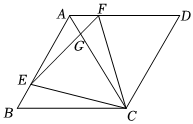3．菱形ABCD中，AB=4，∠B=60°，E，F分別是AB，AD上的動點，且BE=AF，連接EF，交AC于G，則下列結論：①△BEC≌△AFC；②△ECF為等邊三角形；③CE的最小值為2．其中正確的結論是（ ）3發布：2025/6/9 5:30:2組卷：355引用：7難度：0.4