我們知道,可以單獨用正三角形、正方形或正六邊形鑲嵌平面.
如果我們要同時用兩種不同的正多邊形鑲嵌平面,可能設(shè)計出幾種不同的組合方案?
問題解決:
猜想1:是否可以同時用正方形、正八邊形兩種正多邊形組合進(jìn)行平面鑲嵌?
驗證1:在鑲嵌平面時,設(shè)圍繞某一點有x個正方形和y個正八邊形的內(nèi)角可以拼成一個周角.根據(jù)題意,可得方程:90x+(8-2)1808y=360,整理得:2x+3y=8,
我們可以找到方程的正整數(shù)解為x=1 y=2
.
結(jié)論1:鑲嵌平面時,在一個頂點周圍圍繞著1個正方形和2個正八邊形的內(nèi)角可以拼成一個周角,所以同時用正方形和正八邊形兩種正多邊形組合可以進(jìn)行平面鑲嵌.
猜想2:是否可以同時用正三角形和正六邊形兩種正多邊形組合進(jìn)行平面鑲嵌?若能,請按照上述方法進(jìn)行驗證,并寫出所有可能的方案;若不能,請說明理由.
(
8
-
2
)
180
8
x = 1 |
y = 2 |
【考點】平面鑲嵌(密鋪);二元一次方程的應(yīng)用.
【答案】見試題解答內(nèi)容
【解答】
【點評】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/4/20 14:35:0組卷:298引用:2難度:0.3
相似題
-
1.下列正多邊形能夠進(jìn)行鑲嵌的是( )
A.正三角形與正五邊形 B.正方形與正六邊形 C.正方形與正八邊形 D.正六邊形與正八邊形 發(fā)布:2024/10/13 16:0:4組卷:73引用:3難度:0.7 -
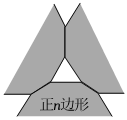 2.如圖是用邊長相等的正三角形和正n邊形兩種地磚鋪設(shè)的部分地面示意圖,則正n邊形的內(nèi)角和為( )
2.如圖是用邊長相等的正三角形和正n邊形兩種地磚鋪設(shè)的部分地面示意圖,則正n邊形的內(nèi)角和為( )
?A.1800° B.1440° C.1080° D.720° 發(fā)布:2024/10/3 15:0:2組卷:127引用:7難度:0.5 -
3.用正三角形和正方形組合能夠鋪滿地面,每個頂點周圍有m個正三角形和n個正方形(m、n為正整數(shù)),則m+n的值為( )
A.4 B.3 C.6 D.5 發(fā)布:2024/12/31 8:30:3組卷:169引用:4難度:0.6


