閱讀理解，自主探究：
“一線三垂直”模型是“一線三等角”模型的特殊情況，即三個等角角度為90°，于是有三組邊相互垂直．所以稱為“一線三垂直模型”．當模型中有一組對應邊長相等時，則模型中必定存在全等三角形．
（1）問題解決：如圖1，在等腰直角△ABC中，∠ACB=90°，AC=BC，過點C作直線DE，AD⊥DE于D，BE⊥DE于E，求證：△ADC≌△CEB；
（2）問題探究：如圖2，在等腰直角△ABC中，∠ACB=90°，AC=BC，過點C作直線CE，AD⊥CE于D，BE⊥CE于E，AD=3.2cm,DE=2.3cm,求BE的長；
（3）拓展延伸：在平面直角坐標系中，A（-1，0），C（1，3），△ABC為等腰直角三角形，∠ACB=90°，AC=BC，求B點坐標．
【考點】三角形綜合題．
【答案】（1）證明見解析過程；
（2）BE=0.9cm；
（3）（-2，5）或（4，1）．
（2）BE=0.9cm；
（3）（-2，5）或（4，1）．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/8/6 8:0:9組卷：411引用：4難度：0.2
相似題
-
1．如圖1，在△ABC中，AB=AC，點D是BC的中點，點E在AD上，連接BE、CE．
（1）求證：BE=CE；
（2）如圖2，若BE的延長線交AC于點F，且BF⊥AC，垂足為F，原題設其它條件不變．求證：∠CAD=∠CBF．
（3）在（2）的條件下，若∠BAC=45°，判斷△CFE的形狀，并說明理由．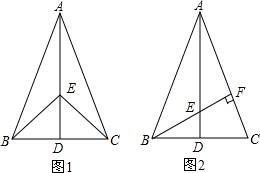
發布：2025/6/3 10:30:2組卷：365引用：4難度：0.3 -
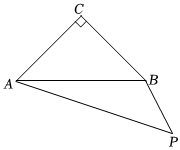2．如圖，在△ABC中，AC=BC，∠ACB=90°，∠APB=45°，連接CP，將線段CP繞點C順時針旋轉90°得到線段CQ，連接AQ．
（1）依題意，補全圖形，并證明：AQ=BP；
（2）求∠QAP的度數；
（3）若N為線段AB的中點，連接NP，請用等式表示線段NP與CP之間的數量關系，并證明．發布：2025/6/3 11:0:2組卷：485引用：6難度：0.1 -
3．已知，在△ABC中，∠ACB=90°，AC=8，tanA=
，D是斜邊AB上一點，連接CD．34
（1）當D是AB的中點時．
①如圖①，求CD的長；
②如圖②，過點D作AB的垂線交AC于點E，求DE的長；
③如圖③，過點A作CD的垂線，交CD的延長線于點M，求sin∠DAM的值；
（2）將△ACD沿直線CD翻折，使得點A落在同一平面內的點A′處，當A′D∥BC時，求AD的長．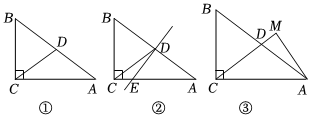
發布：2025/6/3 11:30:1組卷：55引用：2難度：0.4