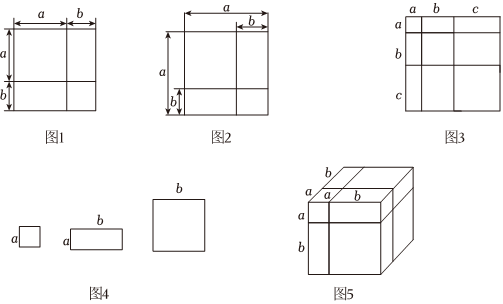
【閱讀材料】“數形結合”是一種非常重要的數學思想方法．比如：在學習整式乘法時，我們通過構造幾何圖形，用“等積法”直觀地推導出了完全平方公式：（a+b）²=a²+2ab+b²（圖1），（a-b）²=a²-2ab+b²（圖2）利用“數形結合”的思想方法，可以從代數角度解決圖形問題，也可以用圖形關系解決代數問題．

【方法應用】根據以上材料提供的方法，完成下列問題：
（1）由圖3可得等式：

a²+b²+c²+2ab+2ac+2bc=（a+b+c）²

a²+b²+c²+2ab+2ac+2bc=（a+b+c）²

；
（2）利用圖3得到的結論，解決問題：若a+b+c=7，ab+ac+bc=14，則a²+b²+c²=

21

21

；
（3）利用圖4解決問題：
①若用其中x張邊長為a的正方形，y張邊長為b的正方形，z張邊長分別為a、b的長方形紙片，拼出一個面積為（3a+b）（a+3b）的長方形（無空隙、無重疊地拼接），則x+y+z=

16

16

；
②若有3張邊長為a的正方形，5張邊長為b的正方形，4張邊長分別為a、b的長方形紙片，從中取出若干張，每種至少取一張．把取出的這些紙片拼成一個正方形（無空隙、無重疊地拼接），則拼成的正方形的邊長最長可以為

（a+2b）

（a+2b）

；
【方法拓展】類似地，利用立體圖形中體積的等量關系也可以得到某些數學公式．
（4）由圖5可得等式：

a³+b³+3a²b+3ab²=（a+b）³

a³+b³+3a²b+3ab²=（a+b）³

．