在研究物體的運動時，復雜的運動可以通過運動的合成與分解將問題“化繁為簡”：比如在研究平拋運動時，我們可以將平拋運動分解為豎直方向的自由落體運動和水平方向的勻速直線運動。如圖所示，在圓柱體內表面距離底面高為h處，給一質量為m的小滑塊沿水平切線方向的初速度v0（俯視如右圖所示），小滑塊將沿圓柱體內表面旋轉滑下。假設滑塊下滑過程中表面與圓柱體內表面緊密貼合，重力加速度為g。
（1）設圓柱體內表面光滑，求：
a.小滑塊滑落到圓柱體底面的時間t；
b.小滑塊滑落到圓柱體底面時速度v的大小；
（2）真實情境中，圓柱體內表面是粗糙的，小滑塊在圓柱體內表面所受到的摩擦力f正比于兩者之間的正壓力N。則對于小滑塊在水平方向的速率v隨時間的變化關系圖象描述正確的為 乙乙。（選填“甲”、“乙”、“丙”）請給出詳細的論證過程。
【考點】平拋運動速度的計算；牛頓第二定律的簡單應用．
【答案】乙
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：153引用：4難度：0.6
相似題
-
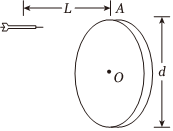1．如圖所示，一位同學做飛鏢游戲，已知圓盤的直徑為d,飛鏢距圓盤的水平距離為L。將飛鏢對準A點以初速度v0水平拋出，在飛鏢拋出的同時，圓盤以角速度ω繞垂直圓盤過盤心O的水平軸勻速轉動。要使飛鏢恰好擊中A點，則飛鏢的初速度和圓盤的角速度應滿足（ ）發布：2024/12/30 0:0:1組卷：46引用：4難度：0.6 -
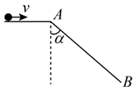2．如圖，在一個光滑水平面上以速度v運動的小球，到達A處時遇到一個足夠長的陡坡AB，已知AB與豎直線之間的夾角為α，重力加速度取g。則小球（ ）發布：2025/1/6 0:30:5組卷：92引用：2難度：0.6 -
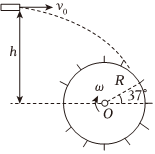3．如圖所示為某種水輪機的示意圖，水平管中流出的水流沖擊水輪機上的某擋板時，水流的速度方向剛好與水輪機上該擋板的線速度方向相同，水輪機圓盤穩定轉動時的角速度為ω，圓盤的半徑為R，水流沖擊某擋板時，該擋板和圓心連線與水平方向夾角為37°，水流速度與該擋板線速度相等，忽略擋板的大小，不計空氣阻力，則水從管口流出的速度v0大小為（ ）發布：2024/12/30 0:0:1組卷：61引用：5難度：0.7