在平面直角坐標(biāo)系xOy中，對(duì)于點(diǎn)A和線段MN，如果點(diǎn)A，O，M，N按逆時(shí)針?lè)较蚺帕袠?gòu)成菱形AOMN，且∠AOM=α，則稱線段MN是點(diǎn)A的“α-相關(guān)線段”．例如，圖1中線段MN是點(diǎn)A的“30°-相關(guān)線段”．
（1）已知點(diǎn)A的坐標(biāo)是（0，2）．
①在圖2中畫(huà)出點(diǎn)A的“30°-相關(guān)線段”MN，并直接寫出點(diǎn)M和點(diǎn)N的坐標(biāo)；
②若點(diǎn)A的“α-相關(guān)線段”經(jīng)過(guò)點(diǎn)（3，1），求α的值；
（2）若存在α，β（α≠β）使得點(diǎn)P的“α-相關(guān)線段”和“β-相關(guān)線段”都經(jīng)過(guò)點(diǎn)（0，4），記PO=t,直接寫出t的取值范圍．
3
【考點(diǎn)】四邊形綜合題．
【答案】（1）①M(fèi)（1，），N（1，+2）．
②60°或120°．
（2）2＜t≤4．
3
3
②60°或120°．
（2）2
2
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書(shū)面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：1219引用：7難度：0.1
相似題
-
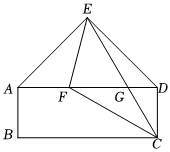1．在五邊形ABCDE中，四邊形ABCD是矩形，△ADE是以E為直角頂點(diǎn)的等腰直角三角形．CE與AD交于點(diǎn)G，將直線EC繞點(diǎn)E順時(shí)針旋轉(zhuǎn)45°交AD于點(diǎn)F．
（1）求證：∠AEF=∠DCE；
（2）判斷線段AB，AF，F(xiàn)C之間的數(shù)量關(guān)系，并說(shuō)明理由；
（3）若FG=CG，且AB=2，求線段BC的長(zhǎng)．發(fā)布：2025/5/24 8:0:1組卷：328引用：2難度：0.2 -
2．[問(wèn)題提出]
正多邊形內(nèi)任意一點(diǎn)到各邊距離之和與這個(gè)正多邊形的半徑R和中心角有什么關(guān)系？
[問(wèn)題探究]
如圖①，△ABC是等邊三角形，半徑OA=R，∠AOB是中心角，P是△ABC內(nèi)任意一點(diǎn)，P到△ABC各邊距離PF、PE、PD分別為h1、h2、h3，設(shè)△ABC的邊長(zhǎng)是a,面積為S．過(guò)點(diǎn)O作OM⊥AB．
∴OM=Rcos∠AOB=Rcos60°，AM=Rsin12∠AOB=Rsin60°，AB=2AM=2Rsin60°12
∴S△ABC=3S△AOB=3×AB×OM=3R2sin60°cos60°①12
∵S△ABC又可以表示為a（h1+h2+h3）②12
聯(lián)立①②得a（h1+h2+h3）=3R2sin60°cos60°12
∴×2Rsin60°（h1+h2+h3）=3R2sin60°cos60°12
∴h1+h2+h3=3Rcos60°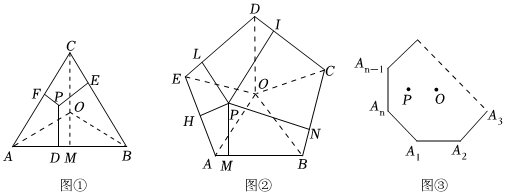
[問(wèn)題解決]
如圖②，五邊形ABCDE是正五邊形，半徑OA=R，∠AOB是中心角，P是△ABC內(nèi)任意一點(diǎn)，P到△ABC各邊距PH、PM、PN、PI、PL分別為h1、h2、h3、h4、h5，參照（1）的分析過(guò)程，探究h1+h2+h3+h4+h5的值與正五邊形ABCDE的半徑R及中心角的關(guān)系．
[性質(zhì)應(yīng)用]
（1）正六邊形（半徑是R）內(nèi)任意一點(diǎn)P到各邊距離之和h1+h2+h3+h4+h5+h6=．
（2）如圖③，正n邊形（半徑是R）內(nèi)任意一點(diǎn)P到各邊距離之和h1+h2+hn-1+hn=．發(fā)布：2025/5/24 8:0:1組卷：149引用：1難度：0.2 -
3．四邊形ABCD為正方形，AB=8，點(diǎn)E為直線BC上一點(diǎn)，射線AE交對(duì)角線BD于點(diǎn)F，交直線CD于點(diǎn)G．
（1）如圖，點(diǎn)E在BC延長(zhǎng)線上．求證：△CFG∽△EFC；
（2）是否存在點(diǎn)E，使得△CFG是等腰三角形？若存在，求BE的長(zhǎng)；若不存在，請(qǐng)說(shuō)明理由．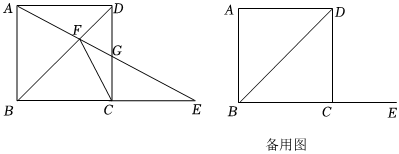
發(fā)布：2025/5/24 7:0:1組卷：57引用：1難度：0.1