[問題提出]:將一個邊長為n(n≥2)的菱形的四條邊n等分,連接各邊對應的等分點,則該菱形被剖分的網格中的平行四邊形的個數和菱形個數分別是多少?
[問題探究]:要研究上面的問題,我們不妨先從特例入手,進而找到一般規律.
探究一:將一個邊長為2的菱形的四條邊分別2等分,連接各邊對應的等分點,則該菱形被剖分的網格中的平行四邊形的個數和菱形個數分別是多少?
如圖1,從上往下,共有2行,我們先研究平行四邊形的個數:
(1)第一行有斜邊長為1,底長為1~2的平行四邊形,共有2+1=3個;
(2)第二行有斜邊長為1,底長為1~2的平行四邊形,共有2+1=3個;
為了便于歸納分析,我們把平行四邊形下面的底在第二行的所有平行四邊形均算作第二行的平行四邊形,以下各行類同第二行.因此底第二行還包括斜邊長為2,底長為1~2的平行四邊形,共有2+1=3個.
即:第二行平行四邊形共有2×3個.
所以如圖1,平行四邊形共有2×3+3-9-(2+1)2.
我們再研究菱形的個數:
分析:邊長為1的菱形共有22個,邊長為2的菱形共有12個,
所以:如圖1,菱形共有22+12=5=16×2×3×5個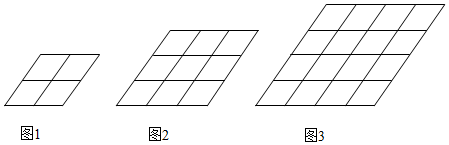
探究二:將一個邊長為3的菱形的四條邊分別3等分,連接各邊對應的等分點,則該菱形被剖分的網格中的平行四邊形的個數和菱形個數分別是多少?
如圖2,從上往下,共有3行,我們先研究平行四邊形的個數:
(1)第一行有斜邊長為1,底長為1~3的平行四邊形,共有3+2+1=6個;
(2)第二行有斜邊長為1,底長為1~2的平行四邊形,共有3+2+1=6個;底在第二行還包括斜邊長為2,底長為1~3的平行四邊形,共有3+2+1=6個,即:第二行平行四邊形共有2×6個.
(3)第三行有斜邊長為1,底長為1~3的平行四邊形,共有3+2+1=6個;底在第三行還包括斜邊長為2,底長為1~3的平行四邊形,共有3+2+1=6個.底在第三行還包括斜邊長為3,底長為1~3的平行四邊形,共有3+2+1=6個.即:第三行平行四邊形共有3×6個.
所以:如圖2,平行四邊形共有3×6+2×6+6=(3+2+1)×6=(3+2+1)2.
我們再研究菱形的個數:
分析:邊長為1的菱形共有32個,邊長為2的菱形共有22個,邊長為3的菱形共有12個.
所以:如圖2,菱形共有32+22+12=14=16×3×4×7個.
探究三:將一個邊長為4的菱形的四條邊4等分,連接對邊對應的等分點,則該菱形被剖分的網格中的平行四邊形的個數和菱形的個數分別是多少呢?
如圖3,從上往下,共有4行,我們先研究平行四邊形的個數:
(1)第一行有斜邊長為1,底長為1~4的平行四邊形,共有4+3+2+1=10個.
(2)第二行有斜邊長為1,底長為1~4的平行四邊形,共有4+3+2+1=10個.底在第二行還包括斜邊長為2,底長為1~4的平行四邊形,共有4+3+2+1=10個.
即:第二行平行四邊形總共有2×10個.
(3)模仿上面的探究,第三行平行四邊形總共有3×(4+3+2+1)3×(4+3+2+1)個;
(4)按照以上規律,第四行平行四邊形總共有4×(4+3+2+1)4×(4+3+2+1)個.
所以:如圖3,平行四邊形總共有(4+3+2+1)2(4+3+2+1)2個.
我們再研究菱形的個數:
分析:邊長為1的菱形共有42個,邊長為2的菱形共有32個,邊長為3的菱形共有22個,邊長為4的菱形共有12個.
所以:如圖3,菱形共有42+32+22+12=30=16×4×5×94×5×9個.(仿照前面的探究,寫成三個整數相乘的形式)
【問題解決】
將一個邊長為n(n≥2)的菱形的四條邊n等分,連接對邊對應的等分點,根據上邊的規律,得出該菱形被剖分的網格中的平行四邊形的個數是(n+n-1+n-2+…+1)2(n+n-1+n-2+…+1)2和菱形的個數分別是16×n(n+1)(2n+1)n(n+1)(2n+1).(用含n的代數式表示).
【問題應用】
將一個邊長為n(n≥2)的菱形的四條邊n等分,連接各邊對應的等分點,若得出該菱形被剖分的網格中的平行四邊形的個數是441個,則n=66.
【拓展延伸】
將一個邊長為n(n≥2)的菱形的四條邊n等分,連接各邊對應的等分點,當該菱形被剖分的網格中的平行四邊形的個數與菱形的個數之比是135:19時,則n=99.
1
6
1
6
1
6
1
6
【考點】規律型:圖形的變化類.
【答案】3×(4+3+2+1);4×(4+3+2+1);(4+3+2+1)2;4×5×9;(n+n-1+n-2+…+1)2;n(n+1)(2n+1);6;9
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/27 10:35:59組卷:157引用:2難度:0.5
相似題
-
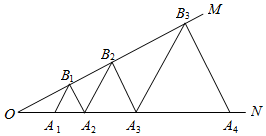 1.如圖,∠MON=30°,點A1、A2、A3…在射線ON上,點B1、B2、B3…在射線OM上,△A1B1A2、△A2B2A3、△A3B3A4…均為等邊三角形,從左起第1個等邊三角形的邊長記為a1,第2個等邊三角形的邊長記為a2.以此類推,若OA1=1,則a2022=.發布:2025/5/25 5:30:2組卷:330引用:5難度:0.5
1.如圖,∠MON=30°,點A1、A2、A3…在射線ON上,點B1、B2、B3…在射線OM上,△A1B1A2、△A2B2A3、△A3B3A4…均為等邊三角形,從左起第1個等邊三角形的邊長記為a1,第2個等邊三角形的邊長記為a2.以此類推,若OA1=1,則a2022=.發布:2025/5/25 5:30:2組卷:330引用:5難度:0.5 -
2.下列圖案由邊長相等的黑、白兩色正方形按一定的規律拼接而成,依此規律,第n個圖形中白色正方形的個數為( )

A.4n+1 B.4n-1 C.3n-2 D.3n+2 發布:2025/5/25 3:30:2組卷:216引用:9難度:0.9 -
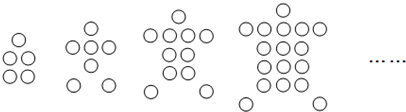
3.將一些相同的“〇”按如圖所示的規律依次擺放,觀察每個“龜圖”的“〇”的個數,則第30個“龜圖”中有 個“〇”.
 發布:2025/5/25 6:30:1組卷:952引用:6難度:0.5
發布:2025/5/25 6:30:1組卷:952引用:6難度:0.5


