我們在七年級曾學(xué)過“兩點(diǎn)之間線段最短”，利用這一知識點(diǎn)也可以解決兩條線段之和最小的相關(guān)問題．
如圖①，已知點(diǎn)A、B在直線l的同一側(cè)，在直線l上求作一點(diǎn)P，使得PA+PB最小．我們只要作點(diǎn)B關(guān)于l的對稱點(diǎn)B′（如圖②），根據(jù)對稱性可知，PB=PB′．因此，求AP+BP最小就相當(dāng)于求AP+PB′最小．顯然，當(dāng)點(diǎn)A、P、B′在同一直線上時(shí)，AP+PB′最小，因此連接AB′，AB′與直線l的交點(diǎn)就是要求的點(diǎn)P．
探究：四邊形ABCD是長方形臺球桌的臺面，有白、黑兩球分別位于點(diǎn)E、F的位置．
（1）如圖③，怎樣擊打白球E，能使它先碰撞臺邊CD，經(jīng)反彈后再擊中黑球F？（畫出白球E經(jīng)過的路線）
（2）如圖④，怎樣擊打白球E，使它能先碰撞臺邊CD，經(jīng)反彈后又碰撞臺邊AB，然后再擊中黑球F？（畫出白球E經(jīng)過的路線）
【答案】（1）先找點(diǎn)E關(guān)于CD的對稱點(diǎn)E′，連接E′F交CD于點(diǎn)M，擊打白球E碰撞臺邊點(diǎn)M，反彈后就能擊中黑球F，圖見解析；
（2）先找點(diǎn)E關(guān)于CD的對稱點(diǎn)E′，點(diǎn)F關(guān)于AB的對稱點(diǎn)F′，連接E′F′交CD于點(diǎn)M，交AB于點(diǎn)N，擊打白球E碰撞臺邊點(diǎn)M，反彈后碰撞臺邊點(diǎn)N，反彈后就能擊中黑球F，圖見解析．
（2）先找點(diǎn)E關(guān)于CD的對稱點(diǎn)E′，點(diǎn)F關(guān)于AB的對稱點(diǎn)F′，連接E′F′交CD于點(diǎn)M，交AB于點(diǎn)N，擊打白球E碰撞臺邊點(diǎn)M，反彈后碰撞臺邊點(diǎn)N，反彈后就能擊中黑球F，圖見解析．
【解答】
【點(diǎn)評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：321引用：1難度：0.6
相似題
-
1．如圖所示，在邊長為1的小正方形網(wǎng)格中，△AOB的頂點(diǎn)都在格點(diǎn)上．
（1）B點(diǎn)關(guān)于y軸的對稱點(diǎn)的坐標(biāo)為 ；
（2）將△AOB向左平移3個(gè)單位長度得到△A1O1B1，請畫出△A1O1B1；
（3）在（2）條件下，點(diǎn)A1的坐標(biāo)為 ；請求出△A1O1B1的面積．發(fā)布：2025/5/23 7:0:1組卷：157引用：4難度：0.3 -
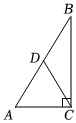2．如圖，在Rt△ABC中，∠ACB=90°，點(diǎn)D是邊AB的中點(diǎn)，連接CD．
（1）求作點(diǎn)E，使點(diǎn)E與點(diǎn)D關(guān)于直線BC對稱（要求：尺規(guī)作圖，不寫作法，保留作圖痕跡）；
（2）在（1）的條件下，連接BE，CE．求證：四邊形BDCE是菱形．發(fā)布：2025/5/23 18:30:2組卷：176引用：1難度：0.6 -
3．如圖，方格紙中每個(gè)小正方形的邊長均為1，△ABC的頂點(diǎn)和線段EF的端點(diǎn)均在小正方形的頂點(diǎn)上．
（1）在方格紙中畫出△ADC，使△ADC與△ABC關(guān)于直線AC對稱（點(diǎn)D在小正方形的頂點(diǎn)上）；
（2）在方格紙中畫出以線段EF為一邊的平行四邊形EFGH（點(diǎn)G，點(diǎn)H均在小正方形的頂點(diǎn)上），且平行四邊形EFGH的面積為4，連接DH，請直接寫出線段DH的長．發(fā)布：2025/5/23 11:0:1組卷：297引用：5難度：0.7