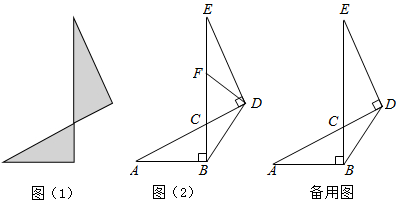
小明將兩個直角三角形紙片如圖（1）那樣拼放在同一平面上，抽象出如圖（2）的平面圖形，∠ACB與∠ECD恰好為對頂角，∠ABC=∠CDE=90°，連接BD，AB=BD，點F是線段CE上一點．
探究發現：
（1）當點F為線段CE的中點時，連接DF（如圖（2）），小明經過探究，得到結論：BD⊥DF．你認為此結論是否成立？是是．（填“是”或“否”）
拓展延伸：
（2）將（1）中的條件與結論互換，即：BD⊥DF，則點F為線段CE的中點．請判斷此結論是否成立．若成立，請寫出證明過程；若不成立，請說明理由．
問題解決：
（3）若AB=6，CE=9，求AD的長．
【考點】三角形綜合題．
【答案】是
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/9 11:0:12組卷：1882引用：11難度：0.6
相似題
-
1．綜合與實踐
問題情境：數學活動課上，王老師出示了一個問題：
如圖1，在△ABC中，D在AB邊上，E在AC邊上，BE與CD相交于點F，∠A=∠EBC+∠DCB．
求證∠A+∠DFE=180°．
獨立思考：（1）請解答王老師提出的問題．
實踐探究：（2）在原有問題條件不變的情況下，王老師增加下面的條件，并提出新問題，請你解答．
“如圖2，若AB=AC．猜想線段BE與線段CD的數量關系，并證明．”
問題解決：（3）數學活動小組同學對上述問題進行研究之后發現，當AE=EF時，若給出圖2中任意兩邊長，則圖2中所有已經用字母標記的線段長均可求．該小組提出下面的問題，請你解答．
“如圖3，在（2）的條件下，若AE=EF=2，EC=3，求AD的長．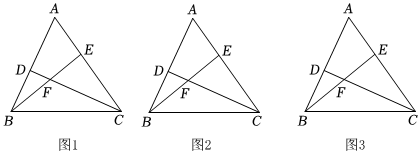
發布：2025/6/9 14:30:1組卷：125引用：1難度：0.1 -
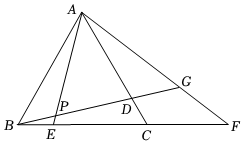2．如圖，等邊△ABC中，D，E分別是AC，BC邊上的點，且BE=CD，連接AE，BD相交于點P，點F在BC的延長線上，且∠CAF=2∠CBD，現給出以下結論：
①AE=BD；
②∠APG=60°；
③DG=2CD；
④CF=CD+GF．
其中正確的是 .（填序號）發布：2025/6/9 14:0:1組卷：480引用：3難度：0.3 -
3．如圖1，在平面直角坐標系中，A（a,0）是x軸正半軸上一點，C是第四象限內一點，CB⊥y軸交y軸負半軸于B（0，b），且|a-3|+（b+4）2=0，S四邊形AOBC=16．
（1）求點C的坐標．
（2）如圖2，設D為線段OB上一動點，當AD⊥AC時，∠ODA的角平分線與∠CAE的角平分線的反向延長線交于點P，求∠APD的度數；（點E在x軸的正半軸）．
（3）如圖3，當點D在線段OB上運動時，作DM⊥AD交BC于M點，∠BMD、∠DAO的平分線交于N點，則點D在運動過程中，∠N的大小是否會發生變化？若不變化，求出其值；若變化，請說明理由．發布：2025/6/9 14:0:1組卷：1193引用：6難度：0.2