綜合與實踐
折紙是一項有趣的活動，折紙活動也伴隨著我們初中數學的學習．在折紙過程中，我們可以研究圖形的運動和性質，也可以在思考問題的過程中，初步建立幾何直觀，現在就讓我們帶著數學的眼光來折紙吧．定義：將紙片折疊，若折疊后的圖形恰能拼合成一個無縫隙、無重疊的矩形，這樣的矩形稱為完美矩形．
（1）操作發現：
如圖①，將△ABC紙片按所示折疊成完美矩形EFGH，若△ABC的面積為12，BC=6，則此完美矩形的邊長FG=33，面積為 66．
（2）類比探究：
如圖②，將平行四邊形ABCD紙片按所示折疊成完美矩形AEFG，若平行四邊形ABCD的面積為20，BC=5，則完美矩形AEFG的周長為 1313．
（3）拓展延伸：
如圖③，將平行四邊形ABCD紙片按所示折疊成完美矩形EFGH，若EF：EH=3：4，AD=15，求此完美矩形的周長為多少．
【考點】四邊形綜合題．
【答案】3；6；13
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/13 8:0:9組卷：260引用：1難度：0.3
相似題
-
1．如圖直角坐標系中直線AB與x軸正半軸、y軸正半軸交于A，B兩點，已知B（0，4），∠BAO=30°，P，Q分別是線段OB，AB上的兩個動點，P從O出發以每秒3個單位長度的速度向終點B運動，Q從B出發以每秒8個單位長度的速度向終點A運動，兩點同時出發，當其中一點到達終點時整個運動結束，設運動時間為t（秒）．
（1）求線段AB的長，及點A的坐標；
（2）t為何值時，△BPQ的面積為2；3
（3）若C為OA的中點，連接QC，QP，以QC，QP為鄰邊作平行四邊形PQCD，
①t為何值時，點D恰好落在坐標軸上；
②是否存在時間t使x軸恰好將平行四邊形PQCD的面積分成1：3的兩部分，若存在，直接寫出t的值．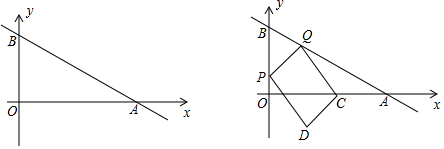
發布：2025/6/20 23:0:1組卷：1027引用：6難度：0.3 -
2．如圖，四邊形ABCD是正方形，E是線段BC上一點，連接AE，將AE繞點E順時針旋轉90°，得到EF，過點F作FG⊥CD于點G．
（1）如圖①，當E是BC的中點時，請直接寫出線段FG和BE的數量關系；
（2）如圖②，當E不是BC的中點時，（1）中的結論是否成立？請說明理由；
（3）若BC=4，CE=2，EF與CD交于點P，請求出CP的長．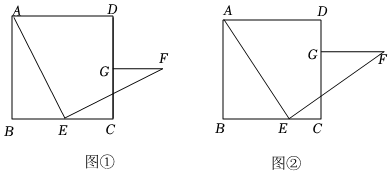
發布：2025/6/20 12:0:2組卷：32引用：1難度：0.1 -
3．如圖1，正方形ABCD，E為平面內一點，且∠BEC=90°，把△BCE繞點B逆時針旋轉90°得△BAG，直線AG和直線CE交于點F．
（1）證明：四邊形BEFG是正方形；
（2）若∠AGD=135°，猜測CE和CF的數量關系，并說明理由；
（3）如圖2，連接DF，若AB=13，CF=17，求DF的長．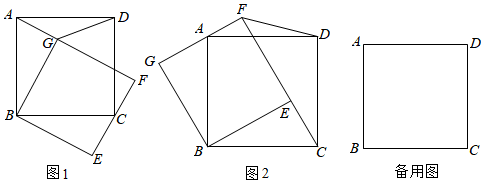
發布：2025/6/20 10:30:1組卷：97引用：1難度：0.1