問題探究與應用實踐
(一)問題探究:
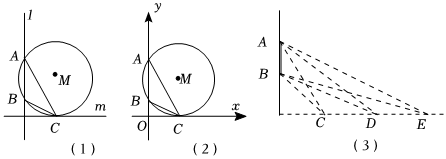
如圖(1),已知直線l與水平視線m互相垂直,A,B在l上,C在m上,∠ACB叫做“視角”,點C叫做“視點”,⊙M是過A,B,C三點的圓.當視點C在直線m上移動時,視角∠ACB的大小會發生改變,可以證明:當視點C恰是⊙M的切點時,視角∠ACB最大,此時觀察AB的效果最佳.當視角∠ACB最大時:分別以直線m,l為x軸和y軸建立平面直角坐標系,如圖(2).
(1)如果此時點A的坐標為(0,4),點B的坐標為(0,1),試求圓心M的坐標及tan∠ACB的值;
(2)如果此時點A,B的坐標分別為(0,a),(0,b),請求出視點C的坐標.(用a,b的代數式表示)
(二)應用實踐:
應用上述結論,讓我們解決如下問題:
如圖(3),AB是廣場上掛的一個大屏幕電視,直線CE是水平視線,屏幕最高點A和最低點B到水平視線CE的距離分別為8米和4米.小明在水平視線上觀看電視節目,當他的視角最大時,視點(在水平視線CE上)到直線AB的距離約是多少?(結果保留一位小數,參考數據:2≈1.414,3≈1.732,5≈2.236)
2
≈
1
.
414
,
3
≈
1
.
732
,
5
≈
2
.
236
【答案】(1)圓心M的坐標為(0,),tan∠ACB的值為;
(2)視點C的坐標(,0);
(3)視點到直線AB的距離約是5.7米.
5
2
3
4
(2)視點C的坐標(
ab
(3)視點到直線AB的距離約是5.7米.
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/21 8:0:10組卷:130引用:2難度:0.5
相似題
-
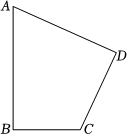 1.如圖,已知一塊四邊形的草地ABCD,其中∠A=60°,∠B=∠D=90°,AB=20m.CD=10m.求這塊草地的面積.發布:2024/12/23 17:0:1組卷:31引用:2難度:0.5
1.如圖,已知一塊四邊形的草地ABCD,其中∠A=60°,∠B=∠D=90°,AB=20m.CD=10m.求這塊草地的面積.發布:2024/12/23 17:0:1組卷:31引用:2難度:0.5 -
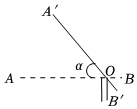 2.某停車場入口的欄桿如圖所示,欄桿從水平位置AB繞點O旋轉A′到A′B′的位置,已知OA=a米,若欄桿的旋轉角∠AOA′=α,則欄桿最外點A升高的高度為( )
2.某停車場入口的欄桿如圖所示,欄桿從水平位置AB繞點O旋轉A′到A′B′的位置,已知OA=a米,若欄桿的旋轉角∠AOA′=α,則欄桿最外點A升高的高度為( )A.atanα米 B.acosα米 C. 米asinaD.asinα米 發布:2025/1/1 6:30:3組卷:129引用:1難度:0.6 -
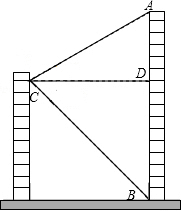 3.小明家所在居民樓的對面有一座大廈AB=74米,為測量這座居民樓與大廈之間的水平距離CD的長度,小明從自己家的窗戶C處測得∠DCA=37°,∠DCB=48°(DC平行于地面).求小明家所在居民樓與大廈的距離CD的長度.
3.小明家所在居民樓的對面有一座大廈AB=74米,為測量這座居民樓與大廈之間的水平距離CD的長度,小明從自己家的窗戶C處測得∠DCA=37°,∠DCB=48°(DC平行于地面).求小明家所在居民樓與大廈的距離CD的長度.
(參考數據:sin37°=,tan37°=35,sin48°=34,tan48°=710)1110發布:2025/1/20 8:0:1組卷:226引用:2難度:0.5


