【教材呈現(xiàn)】蘇科版義務(wù)教育數(shù)學(xué)教科書七下第42頁第20題,是一道研究雙內(nèi)角平分線的夾角和雙外角平分線夾角的數(shù)學(xué)問題,原題如下.
在△ABC中,∠A=n°.
(1)設(shè)∠B、∠C的平分線交于點(diǎn)O,求∠BOC的度數(shù);
(2)設(shè)△ABC的外角∠CBD、∠BCE的平分線交于點(diǎn)O′,求∠BO′C的度數(shù);
(3)∠BOC與∠BO′C有怎樣的數(shù)量關(guān)系?
【問題解決】聰聰對上面的問題進(jìn)行了研究,得出以下答案:
如圖1,在△ABC中,∠A=n°.
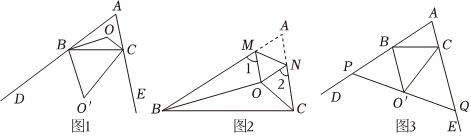
(1)∠ABC、∠ACB的平分線交于點(diǎn)O,則∠BOC的度數(shù)為 90°+12n°90°+12n°;
(2)△ABC的外角∠CBD、∠BCE的平分線交于點(diǎn)O′,則∠BO′C的度數(shù)為 90°-12n°90°-12n°;
(3)∠BOC與∠BO'C的數(shù)量關(guān)系是 ∠BOC+∠BO'C=180°∠BOC+∠BO'C=180°.
(4)【問題深入】:
如圖2,在△ABC中,∠ABC、∠ACB的角平分線交于點(diǎn)O,將△ABC沿MN折疊使得點(diǎn)A與點(diǎn)O重合,請直接寫出∠1+∠2與∠BOC的一個等量關(guān)系式;
(5)如圖3,過△ABC的外角∠CBD、∠BCE的平分線的交點(diǎn)O′,作直線PQ交AD于點(diǎn)P,交AE于點(diǎn)Q.當(dāng)∠APQ=∠AQP時,∠CO′Q與∠ABC有怎樣的數(shù)量關(guān)系?請直接寫出結(jié)果.
90
°
+
1
2
n
°
90
°
+
1
2
n
°
90
°
-
1
2
n
°
90
°
-
1
2
n
°
【考點(diǎn)】三角形內(nèi)角和定理.
【答案】;;∠BOC+∠BO'C=180°
90
°
+
1
2
n
°
90
°
-
1
2
n
°
【解答】
【點(diǎn)評】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/7/11 8:0:9組卷:514引用:2難度:0.5
相似題
-
 1.如圖,D為△ABC內(nèi)一點(diǎn),CD平分∠ACB,BD⊥CD,∠A=∠ABD,若∠DBC=76°,求∠A的度數(shù).發(fā)布:2025/5/30 10:30:1組卷:294引用:1難度:0.7
1.如圖,D為△ABC內(nèi)一點(diǎn),CD平分∠ACB,BD⊥CD,∠A=∠ABD,若∠DBC=76°,求∠A的度數(shù).發(fā)布:2025/5/30 10:30:1組卷:294引用:1難度:0.7 -
 2.如圖,BD是△ABC的角平分線,∠A=50°,點(diǎn)E、F分別在射線BD、BC上.
2.如圖,BD是△ABC的角平分線,∠A=50°,點(diǎn)E、F分別在射線BD、BC上.
(1)若∠ADE=70°,求∠ACB的度數(shù);
(2)若∠E=25°,試判斷CE是否平分∠ACF,并說明理由.發(fā)布:2025/5/30 14:0:1組卷:683引用:3難度:0.5 -
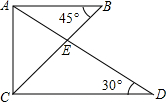 3.一副三角尺拼成如圖所示的圖案,則∠CED的度數(shù)是度.發(fā)布:2025/5/30 11:30:2組卷:259引用:2難度:0.5
3.一副三角尺拼成如圖所示的圖案,則∠CED的度數(shù)是度.發(fā)布:2025/5/30 11:30:2組卷:259引用:2難度:0.5


