已知：如圖1，在正方形ABCD中，E是CD上一點(diǎn)，延長(zhǎng)BC到F，使CF=CE，連接BE、DF．
（1）求證：BE=DF；
（2）如圖2，過點(diǎn)D作DF'⊥DF，交AB邊于點(diǎn)F′，判斷四邊形F′BED是什么特殊四邊形？并說(shuō)明理由．
?

【答案】（1）證明見解析；
（2）四邊形F′BED是平行四邊形．

【解答】

【點(diǎn)評(píng)】

聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。

發(fā)布：2025/5/21 19:30:2組卷：227引用：2難度：0.5

相似題

1．如圖，在正方形ABCD內(nèi)部作等邊△EDC，AE交BC于F點(diǎn)，過E作GH⊥AF，分別交AB、CD于點(diǎn)G，H．則
EH
AF
的值是
．
發(fā)布：2025/5/22 0:0:2組卷：122引用：4難度：0.7
解析
2．如圖（1），在Rt△ABC，∠ACB=90°，分別以AB、BC為一邊向外作正方形ABFG、BCED，連接AD、CF，AD與CF交于點(diǎn)M．
（1）求證：△ABD≌△FBC；
（2）如圖（2），求證：AM²+MF²=AF²．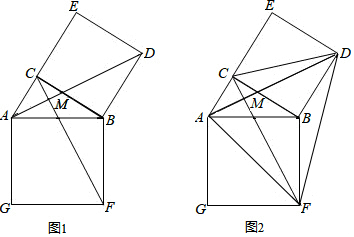
發(fā)布：2025/5/22 1:0:1組卷：705引用：2難度：0.6
解析
3．如圖，點(diǎn)P是正方形ABCD的邊BC上一點(diǎn)，點(diǎn)M是對(duì)角線BD上一點(diǎn)，連接PM并延長(zhǎng)交BA的延長(zhǎng)線于點(diǎn)Q，交AD于點(diǎn)G，取PQ的中點(diǎn)N．連接AN．若AQ=PC，有下面兩個(gè)結(jié)論：①DM=DG，②AN⊥BD，則這兩個(gè)結(jié)論中，正確的是（　　）
A．①對(duì) B．②對(duì) C．①②都對(duì) D．①②都不對(duì)
發(fā)布：2025/5/22 0:30:1組卷：108引用：3難度：0.5
解析

相關(guān)試卷

已知：如圖1，在正方形ABCD中，E是CD上一點(diǎn)，延長(zhǎng)BC到F，使CF=CE，連接BE、DF．（1）求證：BE=DF；（2）如圖2，過點(diǎn)D作DF'⊥DF，交AB邊于點(diǎn)F′，判斷四邊形F′BED是什么特殊四邊形？并說(shuō)明理由．?