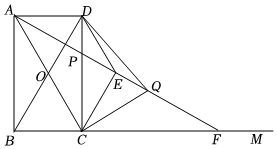
如圖，點C是射線BM上的動點，四邊形ABCD是矩形，對角線AC，BD交于點O，∠DAC的平分線交邊DC于點P，交射線BM于點F，點E在線段PF上（不與點P重合），連接EC，若2∠ECF+∠OBC=180°．
（1）證明AE=EF；
（2）點Q在線段EF上，連接DQ，CQ，DE，當(dāng)∠AQC=∠DAE+∠DEA時，是否存在CP=DQ的情形？請說明理由．
【答案】（1）證明見解析；
（2）不存在CP=DQ的情形，理由見解析．
（2）不存在CP=DQ的情形，理由見解析．
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/9/22 10:0:8組卷：586引用：3難度：0.5
相似題
-
1．如圖，在矩形ABCD中，E，F(xiàn)分別是BC，AD邊上的點，且AE=CF．
（1）求證：△ABE≌△CDF；
（2）當(dāng)AC⊥EF時，判斷四邊形AECF的形狀，并說明理由．發(fā)布：2025/5/24 23:30:2組卷：48引用：1難度：0.6 -
2．如圖，在矩形ABCD中，E、F分別為邊AB、BC的中點，AF與ED、EC分別交于點P、Q．已知AB=6，BC=8，則AP的長為 ．發(fā)布：2025/5/24 19:30:1組卷：211引用：1難度：0.4 -
3．如圖，在矩形ABCD中，E是BC邊上一點，∠AED=90°，∠EAD=30°，F(xiàn)是AD邊的中點，EF=4cm,則BE=cm.發(fā)布：2025/5/24 22:0:1組卷：1588引用：18難度：0.7