教育部印發《義務教育課程方案》和課程標準（2022年版），將勞動從原來的綜合實踐活動課程中獨立出來．某中學為了讓學生體驗農耕勞動，如圖（1）在正方形綠化帶ABCD內修建一個矩形耕種園AEFG，其中點G在AD上，點E在AB上，已知正方形綠化帶ABCD的面積為400m2，AB，AD是墻壁，BC、CD無墻壁．已知矩形耕種園AEFG的面積為正方形花園面積的14，該耕種園借助綠化帶的墻壁，只設置圍欄GF、EF即可．小明用所學的數學知識進行了如下探究．
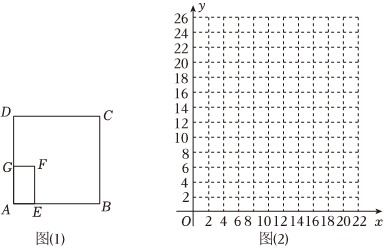
（1）建立數學模型由題意知，此耕種園的面積為400×14=100（m2），設AE=x米，則AG=100x米．設所需圍欄的長度為y米，則y關于x的函數解析式為 y=100x+xy=100x+x；
（2）畫出函數圖象：
1
4
400
×
1
4
=
100
（
m
2
）
AG
=
100
x
y
=
100
x
+
x
y
=
100
x
+
x
| x | 5 | 8 | 10 | 12.5 | 16 | 20 |
| y | 25 | 20.5 | 20 | 20.5 | 22.25 | a |
25
25
；②請根據上表數據，在如圖（2）所示的平面直角坐標系中描點，并畫出y關于x的函數圖象，其中，自變量x的取值范圍是
5≤x≤20
5≤x≤20
；（3）觀察函數圖象，解決問題：
①當所用圍欄20米時，求AE的長；
②若圍欄的長度為b米，則b的取值范圍為
20＜b≤25
20＜b≤25
時，每一個b值都對應兩種圍欄方式．【考點】四邊形綜合題．
【答案】；25；5≤x≤20；20＜b≤25
y
=
100
x
+
x
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/16 15:0:8組卷：114引用：1難度：0.2
相似題
-
1．[問題提出]
正多邊形內任意一點到各邊距離之和與這個正多邊形的半徑R和中心角有什么關系？
[問題探究]
如圖①，△ABC是等邊三角形，半徑OA=R，∠AOB是中心角，P是△ABC內任意一點，P到△ABC各邊距離PF、PE、PD分別為h1、h2、h3，設△ABC的邊長是a,面積為S．過點O作OM⊥AB．
∴OM=Rcos∠AOB=Rcos60°，AM=Rsin12∠AOB=Rsin60°，AB=2AM=2Rsin60°12
∴S△ABC=3S△AOB=3×AB×OM=3R2sin60°cos60°①12
∵S△ABC又可以表示為a（h1+h2+h3）②12
聯立①②得a（h1+h2+h3）=3R2sin60°cos60°12
∴×2Rsin60°（h1+h2+h3）=3R2sin60°cos60°12
∴h1+h2+h3=3Rcos60°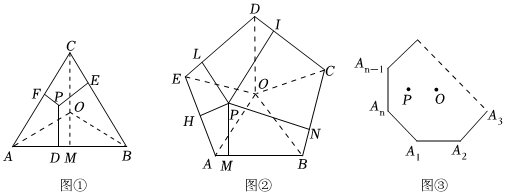
[問題解決]
如圖②，五邊形ABCDE是正五邊形，半徑OA=R，∠AOB是中心角，P是△ABC內任意一點，P到△ABC各邊距PH、PM、PN、PI、PL分別為h1、h2、h3、h4、h5，參照（1）的分析過程，探究h1+h2+h3+h4+h5的值與正五邊形ABCDE的半徑R及中心角的關系．
[性質應用]
（1）正六邊形（半徑是R）內任意一點P到各邊距離之和h1+h2+h3+h4+h5+h6=．
（2）如圖③，正n邊形（半徑是R）內任意一點P到各邊距離之和h1+h2+hn-1+hn=．發布：2025/5/24 8:0:1組卷：149引用：1難度：0.2 -
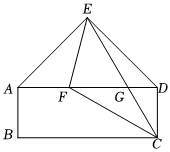2．在五邊形ABCDE中，四邊形ABCD是矩形，△ADE是以E為直角頂點的等腰直角三角形．CE與AD交于點G，將直線EC繞點E順時針旋轉45°交AD于點F．
（1）求證：∠AEF=∠DCE；
（2）判斷線段AB，AF，FC之間的數量關系，并說明理由；
（3）若FG=CG，且AB=2，求線段BC的長．發布：2025/5/24 8:0:1組卷：328引用：2難度：0.2 -
3．四邊形ABCD為正方形，AB=8，點E為直線BC上一點，射線AE交對角線BD于點F，交直線CD于點G．
（1）如圖，點E在BC延長線上．求證：△CFG∽△EFC；
（2）是否存在點E，使得△CFG是等腰三角形？若存在，求BE的長；若不存在，請說明理由．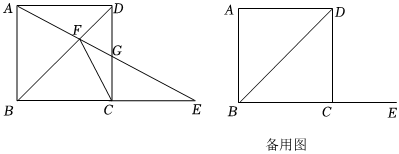
發布：2025/5/24 7:0:1組卷：57引用：1難度：0.1