數學興趣小組在活動時，老師提出了這樣一個問題：
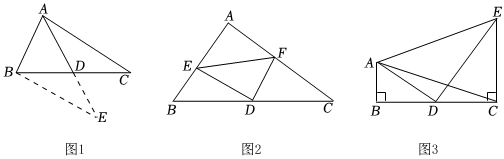
如圖1，在△ABC中，AB=6，AC=10，D是BC的中點，求BC邊上的中線AD的取值范圍．
【閱讀理解】
小明在組內經過合作交流，得到了如下的解決方法：
（1）如圖1，延長AD到點E，使DE=AD，連接BE．根據 SASSAS可以判定△ADC≌△EDB△EDB，得出AC= BEBE．
這樣就能把線段AB，AC，2AD集中在△ABE中．利用三角形三邊的關系，即可得出中線AD的取值范圍是 2＜AD＜82＜AD＜8．
【方法感悟】
當條件中出現“中點”，“中線”等條件時，可以考慮作“輔助線”——把中線延長一倍，構造全等三角形，把分散的已知條件和所求證的結論集中到同一個三角形中，這種作輔助線的方法稱為“中線加倍”法．
【問題解決】
（2）如圖2，在△ABC中，∠A=90°，D是BC邊的中點，∠EDF=90°，DE交AB于點E，DF交AC于點F，連接EF．請判斷BE，CF，EF的數量關系，并說明理由．
【問題拓展】
（3）如圖3，△ABC中，∠B=90°，AB=3，AD是△ABC的中線，CE⊥BC，CE=5，且∠ADE=90°，請直接寫出AE的長．
【考點】三角形綜合題．
【答案】SAS；△EDB；BE；2＜AD＜8
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/10/3 20:0:1組卷：444引用：2難度：0.1
相似題
-
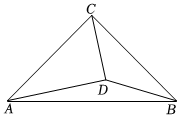1．在△ABC中，∠ACB=90°，AC=BC，點D在△ABC內部，且滿足∠ACD-∠BCD=2∠DAB，若△BCD的面積為13，則CD=．發布：2025/5/22 10:0:1組卷：498引用：3難度：0.3 -
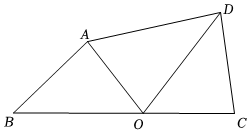2．在四邊形ABCD中，O是邊BC上的一點．若△OAB≌△OCD，則點O叫做該四邊形的“等形點”．
（1）正方形 “等形點”（填“存在”或“不存在”）；
（2）如圖，在四邊形ABCD中，邊BC上的點O是四邊形ABCD的“等形點”．已知CD=4，OA=5，BC=12，連接AC，求AC的長；2
（3）在四邊形EFGH中，EH∥FG．若邊FG上的點O是四邊形EFGH的“等形點”，求的值．OFOG發布：2025/5/22 14:0:1組卷：2058引用：4難度：0.4 -
3．數學課上，李老師出示了如下框中的題目．
如圖1，邊長為6的等邊三角形ABC中，點D沿線段AB方向由A向B運動，點F同時從C出發，以相同的速度沿射線BC方向運動，過點D作DE⊥AC，連接DF交射線AC于點G．求線段AC與EG的數量關系，并說明理由．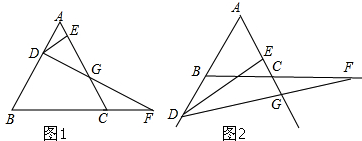
小敏與同桌小聰討論后，進行了如下解答，：
（1）特殊情況?探索結論
當點D恰好在點B處時，易知線段AC與EG的關系是：（直接寫出結論）
（2）特例啟發?解答題目
猜想：線段AC與EG是（1）中的關系，進行證明：
輔助線為“過點D作DH∥BC交AC于點H”，
請你利用全等三角形的相關知識完成解答；
（3）拓展結論?設計新題
如果點D運動到了線段AB的延長線上（如圖2），剛才的結論是否仍成立？請你說明理由．發布：2025/5/22 13:30:1組卷：256引用：3難度：0.1