綜合與實踐——折紙中的數學．
折紙是同學們喜歡的手工活動之一，通過折紙我們可以得到許多美麗的圖形，折紙的過程還蘊含著豐富的數學知識．將長方形紙片（長方形的對邊平行且相等，四個內角都是直角），按下列要求折疊．
（1）如圖1，將長方形紙條沿直線EF折疊，點C落在C′處，點D落在D′處，C'F交AD于點G．
①若∠1=35°，則∠AGC′=110°110°；
②若∠AGC′=3∠1，求∠AGC′的度數．
（2）在圖1的基礎上，將四邊形ABFG沿某一直線折疊，使得AG或BF落在直線GF上，折痕為MN，則折痕MN、EF有怎樣的位置關系，并說明理由．
（3）若AB=3，BC=12，按圖2方式折疊，點C′、G、F、A′在一條直線上．若四邊形B′A′FH的面積記為S1，四邊形D′EGC′的面積記為S2，則S1+S2的值是否有最大值？若有，求出這個值；若沒有，請說明理由．
【考點】四邊形綜合題．
【答案】110°
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/5 16:0:2組卷：184引用：3難度：0.1
相似題
-
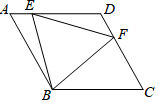1．如圖，已知在四邊形ABCD中，AB=BC=CD=DA=4，且∠ABC=120°，點E、F分別為AD、CD上兩個動點，且∠EBF=60°．
（1）試猜想線段BE、BF之間的關系，并證明你的結論．
（2）求出在點E、F運動的過程中△DEF周長的最小值．
（3）在點E、F運動的過程中△DEF的面積是否存在最大值，如果存在，請你求出△DEF面積的最大值，如果不存在，請說明理由．發布：2025/6/6 22:30:1組卷：349引用：2難度：0.1 -
2．如圖，在△ABC中，AC=3，AB=4，BC=5，P為BC邊上一動點，PG⊥AC于點G，PH⊥AB于點H．
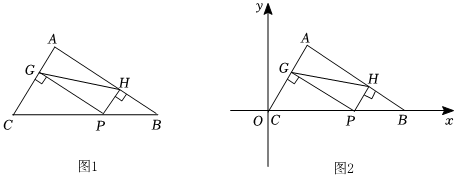
（1）求證：四邊形AGPH是矩形；
（2）在點P的運動過程中，GH的長是否存在最小值？若存在，請求出最小值；若不存在，請說明理由．
（3）如圖2，建立平面直角坐標系，BC和x軸重合，點C和坐標原點重合，以A、B、C、D為頂點的四邊形為平行四邊形，直接寫出所有滿足條件的點D的坐標．發布：2025/6/6 22:30:1組卷：67引用：2難度：0.2 -
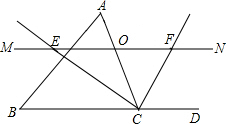3．如圖，在△ABC中，點O是AC邊上一個動點，過點O作直線MN∥BC，設MN交∠BCA的平分線于點E，交∠BCA的外角平分線于點F．
（1）探究OE與OF的數量關系并加以證明；
（2）當點O運動到AC上的什么位置時，四邊形AECF是矩形，請說明理由；
（3）在（2）的基礎上，△ABC滿足什么條件時，四邊形AECF是正方形？為什么？發布：2025/6/6 23:0:1組卷：158引用：4難度：0.3