如圖，∠AOB=120°，射線OC從OA開始，繞點O逆時針旋轉，旋轉的速度為每分鐘20°；射線OD從OB開始，繞點O逆時針旋轉，旋轉的速度為每分鐘5°，OC和OD同時旋轉，設旋轉的時間為t（0≤t≤15）．
（1）當t為何值時，射線OC與OD重合；
（2）當t為何值時，射線OC⊥OD；
（3）試探索：在射線OC與OD旋轉的過程中，是否存在某個時刻，使得射線OC，OB與OD中的某一條射線是另兩條射線所夾角的角平分線？若存在，請求出所有滿足題意的t的取值，若不存在，請說明理由．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：4156引用：7難度：0.3
相似題
-
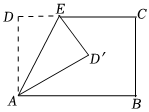1．如圖，將長方形ABCD的一角沿AE折疊，若∠BAD'=30°，那么∠CED'=度．發布：2025/6/3 8:0:2組卷：26引用：1難度：0.7 -
2．如圖，OD平分∠AOB，OE平分∠BOC，∠COD=20°，∠AOB=140°，求∠DOE的度數．發布：2025/6/3 12:0:1組卷：3520引用：11難度：0.3 -
3．點O是直線AB上的一點，∠COD=90°，射線OE是∠BOD的平分線．
（1）∠COD位置如圖1時，試說明∠AOD=2∠COE；
（2）∠COD位置如圖2時，（1）中∠AOD與∠COE的數量關系是否仍然成立？若成立，請說明理由；若不成立，請寫出你得到的結論，并說明理由．
發布：2025/6/3 11:30:1組卷：86引用：1難度：0.4