提出問題：有12個相同的長方體紙盒，它們的長、寬、高分別是4、3、5，現要用這12個紙盒搭成一個大長方體，怎樣搭可使長方體的表面積最小？
分析問題：對于這種問題，我們一般采用復雜問題簡單化的策略，進行由特殊到一般的探究．
探究一：我們以兩個長、寬、高分別是4、3、5的長方體為例進行分析．我們發現，無論怎樣放置這兩個長方體紙盒，搭成的大長方體體積都不變，但是由于擺放位置的不同，它們的表面積會發生變化，經過操作，發現共有3種不同的擺放方式，如圖所示．

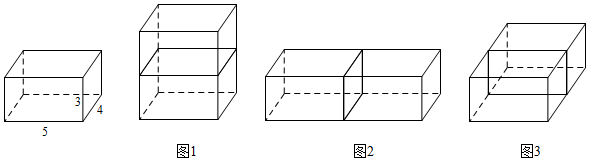
（1）請計算圖1、圖2、圖3中的拼成的新的大長方體的長、寬、高及其表面積，并填充下表：

	長（cm）	寬（cm）	高（cm）	表面積（cm2）
圖1	5	4	6	148
圖2	10	4	3	164
圖3	5	8	3	158 158

根據上表可知，表面積最小的是

圖1

圖1

所示的長方體．（填“圖1”、“圖2”、“圖3”）
探究二：有4個相同的長方體紙盒，它們的長、寬、高分別是5、4、3，現要用這4個紙盒搭成一個大長方體，怎樣搭可使長方體的表面積最小？
先畫出各種擺法的示意圖，再根據各自的表面積得到最小擺法，是一種常規的方法，但比較耗時，也不方便，可以按照下列思路考慮：
在圖1的基礎上繼續擺，要使表面積小，就要重疊大面，得到5×8×6的長方體，這個長方體的表面積為

236

236

；
在圖2的基礎上繼續擺，要使表面積小，就要重疊大面，得到10×4×6的長方體，這個長方體的表面積為

248

248

；
在圖3的基礎上繼續擺，要使表面積小，就要重疊大面，得到5×8×6的長方體，這個長方體的表面積為

236

236

；
綜上所述，有4個相同的長方體紙盒，它們的長、寬、高分別是5、4、3，要用這4個紙盒搭成一個大長方體的表面積最小為

236

236

．
探究三：我們知道，在體積相同的前提下，正方體的表面積最小，所以我們可以盡可能地使所搭成的幾何體為正方體或接近正方體，我們還可以這樣思考：
將4分解質因數，得到1×1×4，或1×2×2兩種情況，通過與小長方體的長寬高5×4×3進行組合：
在L=5×1=5，K=4×2=8，H=3×2=6時，搭成的L×K×H的大長方體最接近正方體，此時表面積最小，表面積為2（L×K+K×H+L×H）=

236

236

（直接寫出結果）．
類比應用：請你仿照探究三的解題思路，解答開始提出的問題：
有12個相同的長方體紙盒，它們的長、寬、高分別是4、3、5，現要用這12個紙盒搭成一個大長方體，怎樣搭可使長方體的表面積最小？
拓展延伸：將168個棱長為1cm的小正方體，拼成一個長方體，使得長方體的表面積達到最小，這個表面積是

188

188

cm²．