若一個整數能表示成a2+b2（a,b是整數）的形式，則稱這個數為“完美數”．例如，5是“完美數”，因為5=12+22，再如M=x2+2xy+2y2=（x+y）2+y2（x,y是整數），所以M也是“完美數”．
（1）請你再寫一個小于10的“完美數”，并判斷41是否為“完美數”；
（2）已知S=x2+9y2+4x-12y+k（x,y是整數，k為常數）要使S為“完美數”，試求出符合條件的一個k值，并說明理由；
（3）如果數m,n都是“完美數”，試說明mn也是“完美數”．
【考點】因式分解的應用．
【答案】（1）41是完美數；
（2）k=8時，S是完美數；
（3）mn是完美數．
（2）k=8時，S是完美數；
（3）mn是完美數．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/10/19 5:0:1組卷：669引用：3難度：0.7
相似題
-
1．設a、b為任意不相等的正數，且
，x=b2+4a，則x、y一定（ ）y=a2+4b發布：2025/5/25 18:30:1組卷：50引用：1難度：0.6 -
2．一個四位正整數P滿足千位上的數字比百位上的數字大2，十位上的數字比個位上的數字大2，千位上的數字與十位上的數字不相等且各個數位上的數字均不為零，則稱P為“雙減數”，將“雙減數”P的千位和十位數字組成的兩位數與百位和個位數字組成的兩位數的和記為M（P），將“雙減數”P的千位和百位數字組成的兩位數與十位和個位數字組成的兩位數的差記為N（P），并規定F（P）=
．M（P）N（P）
例如：四位正整數7564，∵7-5=6-4=2，且7≠6，∴7564是“雙減數”，此M（7564）=76+54=130，N（7564）=75-64=11，∴F（7564）=．13011
（1）填空：F（3186）=，并證明對于任意“雙減數”A，N（A）都能被11整除；
（2）若“雙減數”P為偶數，且M（P）-N（P）能被6整除，求滿足條件的所有“雙減數”P，并求F（P）的值．發布：2025/5/25 17:0:1組卷：383引用：2難度：0.5 -
3．【實踐操作】
小明在學習了八下數學課本中“因式分解”章節，用各若立體方塊進行實踐操作探究，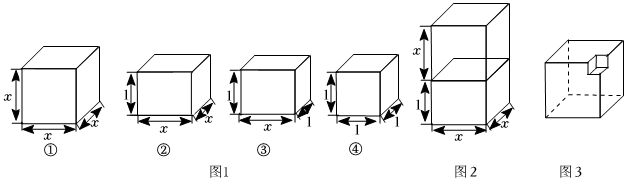
【溫故知新】
如圖，現有編號為①②③④的四種長方體各若干塊，現取其中兩塊拼成一個大長方體如圖2，據此寫出一個多項式的因式分解：．
【問題解決】
如圖，若要用這四種長方體拼成一個棱長為（x+1）的正方體，需要②號長方體 個，③號長方體 個，據此寫出一個多項式的因式分解：．
【拓展與延伸】
如圖3，在一個棱長為a的正方體中挖出一個棱長為b的正方體，據此寫出a3-b3=．發布：2025/5/25 16:0:2組卷：217引用：2難度：0.4