問題背景：
如圖1：在四邊形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°．E，F分別是BC，CD上的點．且∠EAF=60°．探究圖中線段BE，EF，FD之間的數量關系．
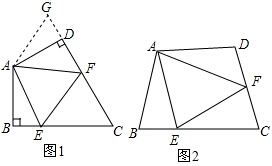
（1）小王同學探究此問題的方法是：延長FD到點G．使DG=BE．連接AG，先證明△ABE≌△ADG，再證明△AEF≌△AGF，可得出結論，他的結論應是 EF=BE+DFEF=BE+DF；（并寫出證明過程）
探索延伸：
（2）如圖2，若在四邊形ABCD中，AB=AD，∠B+∠D=180°．E，F分別是BC，CD上的點，且∠EAF=12∠BAD，上述結論是否仍然成立，并說明理由．
1
2
【答案】EF=BE+DF
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/21 17:0:12組卷：420引用：7難度：0.6
相似題
-
1．如圖，在△ABC中，∠BAC=90°，延長BA到點D，使AD=AB，點E、F分別為BC、AC的中點，請你在圖中找出一組相等關系，使其滿足上述所有條件，并加以證明．12發布：2025/1/24 8:0:2組卷：4引用：1難度：0.5 -
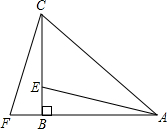2．如圖，在△ABC中，AB=CB，∠ABC=90°，F為AB延長線上一點，點E在線段BC上，且AE=CF．
求證：∠AEB=∠CFB．發布：2025/1/24 8:0:2組卷：454引用：4難度：0.7 -
3．如圖，在Rt△ABC中，∠C=∠BED=90°，且CD=DE，AD=BD，則∠B=．發布：2025/1/28 8:0:2組卷：10引用：0難度：0.7