如圖，在Rt△ABC中，∠ACB=90°，E為AC上一點，且AE=BC，過點A作AD⊥CA，垂足為A，且AD=AC，AB、DE交于點F
（1）判斷線段AB與DE的數(shù)量關(guān)系和位置關(guān)系，并說明理由
（2）連接BD、BE，若設(shè)BC=a,AC=b,AB=c,請利用四邊形ADBE的面積證明勾股定理．
【考點】全等三角形的判定與性質(zhì)；勾股定理的證明．
【答案】見試題解答內(nèi)容
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：449引用：11難度：0.3
相似題
-
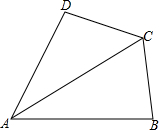1．如圖，在四邊形ABCD中，CB=CD，∠BAD=60°，∠ABC+∠ADC=180°，連接AC，AC=2，則四邊形ABCD的面積是．3發(fā)布：2025/5/25 14:30:1組卷：159引用：2難度：0.5 -
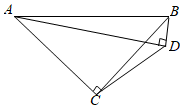2．如圖，四邊形ABDC中，AC=BC，∠ACB=90°，AD⊥BD于點D．若BD=2，CD=4，則線段AB的長為 ．2發(fā)布：2025/5/25 17:0:1組卷：2120引用：5難度：0.4 -
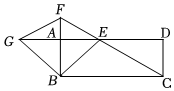3．如圖，在矩形ABCD中，AB=1，AD=3，E為AD邊的一動點（不與端點重合），連接CE并延長，交BA的延長線于點F，延長EA至點G，使AG=AE；分別連接BE，BG，F(xiàn)G．
（1）在點E的運動過程中，四邊形BEFG能否成為菱形？請判斷并說明理由．
（2）若△BAE與△EDC相似，求AE的長．發(fā)布：2025/5/25 17:0:1組卷：122引用：1難度：0.5