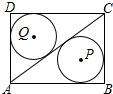
如圖，矩形ABCD中，AB=4，BC=3，連接AC，⊙P和⊙Q分別是△ABC和△ADC的內切圓，則PQ的長是（ ）
【考點】三角形的內切圓與內心；矩形的性質．
【答案】B
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/27 14:0:0組卷：2666引用：6難度：0.7
相似題
-
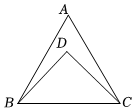1．如圖，△ABC和△DBC中，點D在△ABC內，AB=AC=BC=2，DB=DC，且∠D=90°，則△ABC的內心和△DBC的外心之間的距離為（ ）發布：2025/5/24 14:30:1組卷：327引用：2難度：0.5 -
2．如圖，△ABC的內切圓⊙O與BC，CA，AB分別相切于點D，E，F，且AB=5，BC=13，CA=12，則陰影部分的面積為（結果保留π）．發布：2025/5/24 15:30:1組卷：673引用：7難度：0.5 -
3．已知在Rt△ABC中，∠C=90°，cotA=
，那么以邊AC長的65倍為半徑的圓A與以BC為直徑的圓的位置關系是（ ）32發布：2025/5/24 14:0:2組卷：69引用：3難度：0.5