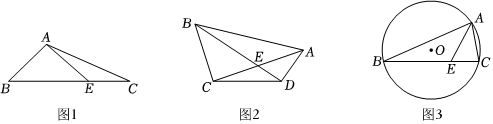
定義：三角形一邊上的點將該邊分為兩條線段，且這兩條線段的積等于這個點與該邊所對頂點連線長度的平方，則稱這個點為三角形該邊的“奇點”．如圖1，△ABC中，點E是BC邊上一點，連接AE，若AE2=BE?CE，則稱點E是△ABC中BC邊上的“奇點”．
?（1）如圖2，已知，在四邊形ABCD中，BD平分AC于點E，∠CAD=∠CBD，求證：點E是△ABD中BD邊上的“奇點”：
（2）如圖3，△ABC是⊙O的內(nèi)接三角形，點E是△ABC中BC邊上的“奇點”，若∠BAE=∠CAE，求AE2AB?AC的值；
（3）在Rt△ABC中，∠A=90°，AB=45，BC=10，點E是BC邊上的“奇點”，求線段BE的長．
A
E
2
AB
?
AC
AB
=
4
5
【考點】相似形綜合題．
【答案】（1）證明見解析；
（2）；
（3）8或5．
（2）
1
2
（3）8或5．
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2024/7/1 8:0:9組卷：209引用：1難度：0.5
相似題
-
1．在Rt△ABC中，∠ACB=90°，tan∠ABC=a,D是BC上一點（不與點B，C重合），連接AD，過點C作CE⊥AD于點E，連接BE并延長，交AC于點F．
（1）如圖1，當a=1時，
①求證：∠ECD＜45°；
②求證：；BEEF=CDCF
（2）如圖2，若D是BC的中點，求tan∠CEF的值（用含a的代數(shù)式表示）．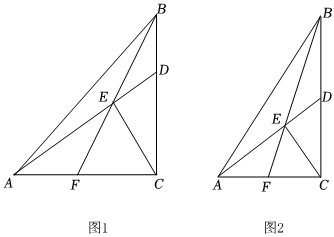
發(fā)布：2025/6/5 6:0:2組卷：335引用：4難度：0.3 -
2．綜合與實踐
我們在沒有量角器或三角尺的情況下，用折疊特殊矩形紙片的方法進行如下操作也可以得到幾個相似的含有30°角的直角三角形．
實踐操作：
第一步：如圖①，矩形紙片ABCD的邊長AB=，將矩形紙片ABCD對折，使點D與點A重合，點C與點B重合，折痕為EF，然后展開，EF與CA交于點H．5
第二步：如圖②，將矩形紙片ABCD沿過點C的直線再次折疊，使CD落在對角線CA上，點D的對應(yīng)點D'恰好與點H重合，折痕為CG，將矩形紙片展平，連接GH．
問題解決：
（1）在圖②中，sin∠ACB=，=；EGCG
（2）在圖②中，CH2=CG?；從圖②中選擇一條線段填在空白處，并證明你的結(jié)論；
拓展延伸：
（3）將上面的矩形紙片ABCD沿過點C的直線折疊，點D的對應(yīng)點D′落在矩形的內(nèi)部或一邊上，設(shè)∠DCD′=α，若0°＜α≤90°，連接D′A，D′A的長度為m,則m的取值范圍是 ．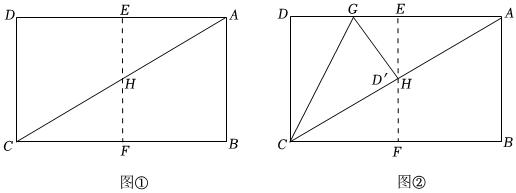
發(fā)布：2025/6/5 1:30:2組卷：279引用：2難度：0.2 -
3．（1）如圖所示，矩形ABCD中，BC=2AB，將矩形ABCD繞點B逆時針旋轉(zhuǎn)90°，得到新的矩形BEFH，連接FD，EC，線段EC交FD于點G，連BG．
①請直接寫出線段FB和BD的數(shù)量關(guān)系 ，位置關(guān)系 ；
②求證：FD=2BG．
（2）如圖2所示，Rt△BCD中，∠C=90°，BC=3CD，將Rt△BCD繞點B逆時針旋轉(zhuǎn)α°，得到新的Rt△BEF，連接EC，F(xiàn)D，線段EC，F(xiàn)D相交于點G，點O為線段BD中點，連OG，在Rt△BCD旋轉(zhuǎn)的過程中，是否發(fā)生改變？如果不變，請求出OGBC的值；如果發(fā)生改變，請說明理由．OGBC發(fā)布：2025/6/5 7:30:1組卷：455引用：5難度：0.1
相關(guān)試卷