當前位置：
試題詳情
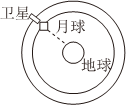2018年6月14日。承擔嫦娥四號中繼通信任務的“鵲橋”中繼星抵達繞地月第二拉格朗日點的軌道。第二拉格朗日點是地月連線延長線上的一點，處于該位置上的衛星與月球同步繞地球公轉，則該衛星的（ ）
【考點】拉格朗日點；牛頓第二定律與向心力結合解決問題．
【答案】B；D
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/12/29 16:0:1組卷：156引用：7難度：0.5
相似題
-
1．如圖所示，地球和月球組成“地月雙星系統”，兩者繞共同的圓心C點（圖中未畫出）做周期相同的圓周運動。數學家拉格朗日發現，處在如圖所示拉格朗日點的航天器在地球和月球引力的共同作用下可以繞“地月雙星系統”的圓心C點做周期相同的圓周運動，從而使地、月、航天器三者在太空的相對位置保持不變。不考慮航天器對“地月雙星系統”的影響，不考慮其他天體對該系統的影響。已知地球質量為M，月球質量為m,地球與月球球心距離為d。則下列說法正確的是（ ）發布：2024/11/3 7:30:1組卷：237引用：5難度：0.4 -
2．今年，我國將發射“嫦娥四號”，實現人類首次月球背面軟著陸。為了實現地球與月球背面的通信，將先期發射一枚拉格朗日L2點中繼衛星。拉格朗日L2點是指衛星受太陽、地球兩大天體引力作用，能保持相對靜止的點，是五個拉格朗日點之一，位于日地連線上、地球外側約1.5×106km處。已知拉格朗日L2點與太陽的距離約為1.5×108km,太陽質量約為2.0×1030kg,地球質量約為6.0×1024kg.在拉格朗日L2點運行的中繼衛星，受到太陽引力F1和地球引力F2大小之比為（ ）發布：2024/12/30 1:0:6組卷：122引用：4難度：0.9 -
3．在兩個大物體引力場空間中存在著一些點，在這些點處的小物體可相對于兩個大物體基本保持靜止，這些點稱為拉格朗日點。中國探月工程中的“鵲橋號”中繼衛星是世界上首顆運行于地月拉格朗日L2點的通信衛星，如圖所示，該衛星在幾乎不消耗燃料的情況下與月球同步繞地球做圓周運動，關于處于拉格朗日L1和L2點上的兩顆同等質量的衛星，下列說法正確的是（ ）發布：2024/7/22 8:0:9組卷：120引用：2難度：0.5