在平面直角坐標系中,我們不妨把橫坐標和縱坐標相等的點叫“相等點”,例如點(1,1),(0.5,0.5),(-2,-2),(-2,-2)…都是“相等點”,顯然“相等點”有無數個.
(1)若點P(3,m)是反比例函數y=nx(n為常數,n≠0)的圖象上的“相等點”,求這個反比例函數的解析式.
(2)一次函數y=kx-1(k為常數,k≠0)的圖象上存在“相等點”嗎?若存在,請用含k的式子表示出“相等點”的坐標,若不存在,說明理由;
(3)若二次函數y=2x2+bx+c(b,c為常數)的圖象上有且只有一個“相等點”,令t=b2+8c,當0≤b≤2時,求t的取值范圍.
2
2
n
x
【答案】見試題解答內容
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/27 10:35:59組卷:260引用:2難度:0.6
相似題
-
1.已知y-2與x成反比例,當x=3時,y=1,則y與x的函數關系式為
.發布:2025/6/22 17:30:1組卷:705引用:35難度:0.7 -
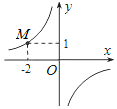 2.如圖,某反比例函數的圖象過點M(-2,1),則此反比例函數表達式為( )
2.如圖,某反比例函數的圖象過點M(-2,1),則此反比例函數表達式為( )A.y= 2xB.y=- 2xC.y= 12xD.y=- 12x發布:2025/6/22 19:0:1組卷:677引用:71難度:0.9 -
3.已知y=y1-y2,其中y1與x成反比例,y2與x2成正比例,且當x=1時,y=3;當x=-2時,y=-15.
(1)求y與x的函數關系式;
(2)當x=2時,求y的值.發布:2025/6/22 21:0:10組卷:76引用:1難度:0.6


