觀察下列各式：32-1=2×4，42-1=3×5，52-1=4×6…將你猜想到的規(guī)律用一個式子來表示：（n+2）2-1=n+1?n+3（n+2）2-1=n+1?n+3．
3
2
-
1
=
2
×
4
4
2
-
1
=
3
×
5
，
5
2
-
1
=
4
×
6
（
n
+
2
）
2
-
1
=
n
+
1
?
n
+
3
（
n
+
2
）
2
-
1
=
n
+
1
?
n
+
3
【考點(diǎn)】規(guī)律型：數(shù)字的變化類．
【答案】
（
n
+
2
）
2
-
1
=
n
+
1
?
n
+
3
【解答】
【點(diǎn)評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/4/20 14:35:0組卷：196引用：37難度：0.5
相似題
-
1．已知：a是不為1的有理數(shù)，我們把
稱為a的差倒數(shù)．如：5的差倒數(shù)是11-a，-3的差倒數(shù)是11-5=-14，已知11-（-3）=14，a2是a1的差倒數(shù)，a3是a2的差倒數(shù)，a4是a3的差倒數(shù)，…，以此類推，a2020的值為（ ）a1=32發(fā)布：2025/6/21 13:0:29組卷：104引用：3難度：0.6 -
2．一列數(shù)按某規(guī)律排列如下
，…若第n個數(shù)為11，12，21，13，22，31，14，23，32，41，則n=．56發(fā)布：2025/6/21 12:0:1組卷：1487引用：3難度：0.3 -
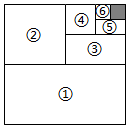3．如圖，將一個邊長為1的正方形紙片分割成7個部分，部分1是邊長為1的正方形紙片面積的一半，部分2是部分1面積的一半，部分3是部分2面積的一半，依此類推．陰影部分的面積是 ；受此啟發(fā)，則+12+14+…+18的值為 ．126發(fā)布：2025/6/21 12:0:1組卷：974引用：3難度：0.8