擺動是生活中常見的運動形式,秋千、鐘擺的運動都是我們熟悉的擺動。擺的形狀各異,卻遵循著相似的規律。
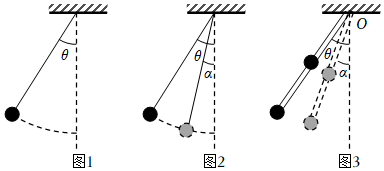
(1)如圖1所示,一個擺的擺長為L,小球質量為m,拉起小球使擺線與豎直方向夾角為θ時將小球由靜止釋放,忽略空氣阻力。
a.求小球運動到最低點時繩對球的拉力的大小F。
b.如圖2所示,當小球運動到擺線與豎直方向夾角為α(α<θ)時,求此時小球的角速度大小ω1。
(2)如圖3所示,長為L的輕桿,一端可繞固定在O點的光滑軸承在豎直平面內轉動,在距O點為L2和L處分別固定一個質量為m、可看作質點的小球,忽略輕桿的質量和空氣阻力。
a.將桿與小球組成的系統拉到與豎直方向成θ角的位置由靜止釋放,當系統向下運動到與豎直方向夾角為α(α<θ)時,求此時系統的角速度大小ω2。
b.若θ較小,系統的運動可看作簡諧運動,對比ω2和ω1的表達式,參照單擺的周期公式T=2πLg,寫出此系統做簡諧運動的周期的表達式,并說明依據。
L
2
L
g
【考點】桿球類模型及其臨界條件.
【答案】(1)a.小球運動到最低點時繩對球的拉力的大小為mg (3-2cosθ)。
b.此時小球的角速度大小為。
(2)a.此時系統的角速度大小為。
b.此系統做簡諧運動的周期的表達式為T'=2,依據見解析。
b.此時小球的角速度大小為
2
g
(
cosα
-
cosθ
)
L
(2)a.此時系統的角速度大小為
12
g
(
cosα
-
cosθ
)
5
L
b.此系統做簡諧運動的周期的表達式為T'=2
π
5
L
6
g
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/4/20 14:35:0組卷:404引用:5難度:0.3
相似題
-
1.一輕桿下端固定一質量為M的小球,上端連在軸上,并可繞軸在豎直平面內運動,不計空氣阻力。在最低點給小球水平速度v0時,剛好能到達最高點,若小球在最低點的瞬時速度從v0不斷增大,則可知( )
A.小球在最高點對桿的作用力不斷增大 B.小球在最高點對桿的作用力先減小后增大 C.小球在最高點對桿的作用力不斷減小 D.小球在最高點對桿的作用力先增大后減小 發布:2024/9/27 0:0:1組卷:73引用:2難度:0.8 -
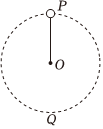 2.如圖所示,一長為0.1m的輕桿的一端固定在位于O點的水平轉軸上,另一端固定一質量為0.1kg的小球(可視為質點),輕桿隨轉軸在豎直平面內做圓周運動,P是圓周上的最高點,Q為最低點。已知重力加速度g取10m/s2,不計空氣阻力,下列說法正確的是( )?
2.如圖所示,一長為0.1m的輕桿的一端固定在位于O點的水平轉軸上,另一端固定一質量為0.1kg的小球(可視為質點),輕桿隨轉軸在豎直平面內做圓周運動,P是圓周上的最高點,Q為最低點。已知重力加速度g取10m/s2,不計空氣阻力,下列說法正確的是( )?A.當小球運動到與O點等高的水平位置時,桿對小球的作用力為零 B.若小球剛好能經過最高點P,則此時桿對小球的作用力為零 C.若小球經過P點時桿對小球的作用力大小等于0.36N,則此時小球的速度大小一定等于0.8m/s D.若小球經過Q點時桿對小球的作用力大小等于5N,則此時小球的速度大小一定等于2m/s 發布:2024/10/13 0:0:1組卷:371引用:1難度:0.5 -
3.一根長L=60cm的輕桿一端固定著一個小球,小球在豎直平面內做圓周運動.已知球的質量m=0.5kg,求:(g=10m/s2)
(1)試確定到達最高點時向心力的最小值;
(2)小球到達能夠最高點繼續做圓周運動的最小速度;
(3)當小球在最高點時的速度為3m/s時,輕桿對小球的作用力.發布:2024/9/27 4:0:1組卷:7引用:2難度:0.3
相關試卷


