如圖，△ABC中，∠ACB=90°，AB=5cm,BC=4cm,過點A作射線l∥BC，若點P從點A出發，以每秒2cm的速度沿射線l運動，設運動時間為t秒（t＞0），作∠PCB的平分線交射線l于點D，記點D關于射線CP的對稱點是點E，連接AE、PE、BP．
（1）求證：PC=PD；
（2）當△PBC是等腰三角形時，求t的值；
（3）是否存在點P，使得△PAE是直角三角形，如果存在，請直接寫出t的值，如果不存在，請說明理由．
【考點】幾何變換綜合題．
【答案】（1）證明見解答過程；
（2）t=1或或或；
（3）存在，t=或．
（2）t=1或
7
2
4
-
7
2
4
+
7
2
（3）存在，t=
3
2
3
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/10/6 2:0:1組卷：862引用：3難度：0.3
相似題
-
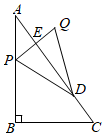1．如圖，在△ABC中，∠ABC=90°，AB=4，BC=3．點P從點A出發，沿折線AB-BC以每秒5個單位長度的速度向點C運動，同時點D從點C出發，沿CA以每秒2個單位長度的速度向點A運動，點P到達點C時，點P、D同時停止運動．當點P不與點A，C重合時，作點P關于直線AC的對稱點Q，連接PQ交AC于點E，連接DP、DQ．設點P的運動時間為t秒．
（1）當點P與點B重合時，求t的值；
（2）用含t的代數式表示線段CE的長；
（3）當△PDQ為等腰直角三角形時，求t的值．發布：2025/5/25 12:30:1組卷：196引用：4難度：0.3 -
2．【問題提出】
（1）如圖①，在矩形ABCD中，點P、Q分別在線段AD、BC上，點B與點E關于PQ對稱，點E在線段AD，連接BP、EQ、PQ交BE于點O，則四邊形PBQE的形狀是 ；
【問題探究】
（2）如圖②，在矩形ABCD中，AB=3，點P、Q分別在線段AB、BC上，點B與點E關于PQ對稱，點E在線段AD上，，求PQ的長；AE=5
【問題解決】
（3）如圖③，有一塊矩形空地ABCD，AB=60m,BC=80m,點P是一個休息站且在線段AB上，AP=40m,點Q在線段BC上，現要在點B關于PQ對稱的點E處修建口水井，并且修建水渠AE和CE，以便于在四邊形空地AECD上種植花草，余下部分貼上地磚．種植花草的四邊形空地AECD的面積是否存在最小值，若存在，請求出最小值，若不存在，請說明理由．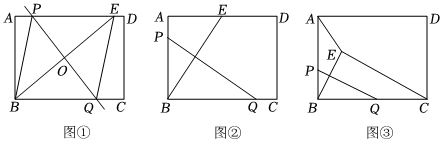
發布：2025/5/25 13:0:1組卷：154引用：1難度：0.2 -
3．在△ABC中，∠C=90°，AC=BC=2，將一塊三角板的直角頂點放在斜邊AB的中點P處，將此三角板繞點P旋轉，三角板的兩直角邊分別交射線AC、CB于點D、點E，圖①，②，③是旋轉得到的三種圖形．
（1）觀察線段PD和PE之間有怎樣的大小關系？并以圖②為例，并加以證明；
（2）觀察線段CD、CE和BC之間有怎樣的數量關系？并以圖③為例，并加以證明；
（3）△PBE是否能成為等腰三角形？若能，請直接寫出∠PEB的度數；若不能，請說明理由．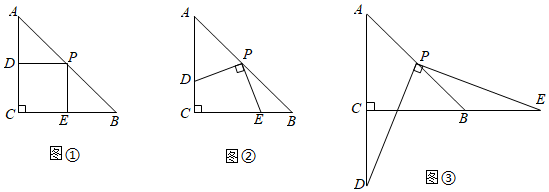
發布：2025/5/25 11:0:2組卷：950引用：4難度：0.2