如圖為某同學設計的帶電粒子的聚焦和加速裝置示意圖。位于S點的粒子源可以沿紙面內與SO1(O1為圓形磁場的圓心)的夾角為θ(θ≤60°)的方向內均勻地發射速度為v0=10m/s、電荷量均為q=-2.0×10-4C、質量均為m=1.0×10-6kg的粒子,粒子射入半徑為R=0.1m的圓形區域勻強磁場。已知粒子源在單位時間發射N=2.0×105個粒子,圓形區域磁場方向垂直紙面向里,沿著SO1射入圓形區域磁場的粒子恰好沿著水平方向射出磁場。粒子數控制系統是由豎直寬度為L、且L在0≤L≤2R范圍內大小可調的粒子通道構成,通道豎直寬度L的中點與O1始終等高。聚焦系統是由有界勻強電場和有界勻強磁場構成,勻強電場的方向水平向右、場強E=0.625N/C,邊界由x軸、曲線OA和直線GF(方程為:y=-x+0.4(m))構成,勻強磁場方向垂直紙面向里、磁感應強度B=0.25T,磁場的邊界由x軸、直線GF、y軸構成,已知所有經過聚焦系統的粒子均可以從F點沿垂直x軸的方向經過一段真空區域射入加速系統。加速系統是由兩個開有小孔的平行金屬板構成,兩小孔的連線過P點,上下兩板間電勢差U=-10kv,不計粒子的重力和粒子間的相互作用力。求:
(1)圓形磁場的磁感應強度B0;
(2)當L=R時,求單位時間進入聚焦系統的粒子數N0;
(3)若進入加速系統內粒子的初速度均忽略不計,設從加速系統射出的粒子在測試樣品中運動所受的阻力f與其速度v關系為f=kv(k=0.2N?s?m-1),求粒子在樣品中可達的深度d;
(4)曲線OA的方程。

【答案】(1)圓形磁場的磁感應強度為0.5T;
(2)當L=R時,單位時間進入聚焦系統的粒子數為105;
(3)粒子在樣品中可達的深度為10-2m;
(4)曲線OA的方程為10y2-y-x=0。
(2)當L=R時,單位時間進入聚焦系統的粒子數為105;
(3)粒子在樣品中可達的深度為10-2m;
(4)曲線OA的方程為10y2-y-x=0。
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/9/29 3:0:2組卷:106引用:4難度:0.5
相似題
-
1.如圖1所示,在xOy坐標系中,兩平行極板P、Q垂直于y軸且關于x軸對稱,極板長度和板間距均為l,緊靠極板的右邊緣的有界勻強磁場區域由ΔAB0和矩形0BCD構成,其中∠OAB=60°,OD=OA.磁場方向垂直于xOy平面向里,D、A位于y軸上。位于極板左側的粒子源沿x軸向右接連發射質量為m,電荷量為+q、速度相同的帶電粒子,現在0~3t0時間內兩板間加上如圖2所示的電壓,已知t=0時刻進入兩板間的粒子,在t0時刻射入磁場時,恰好不會從磁場邊界射出磁場區域且圓心在x軸上,上述l、m、q、t0為已知量,U0=
,不考慮P、Q兩板電壓的變化對磁場的影響,也不考慮粒子的重力及粒子間的相互影響,求:ml2qt02
(1)t=0時刻進入兩板間的帶電粒子射入磁場時的速度;
(2)勻強磁場的磁感應強度的大小及磁場區域的面積;
(3)t=t0時刻進入兩板間的帶電粒子在勻強磁場中運動的時間。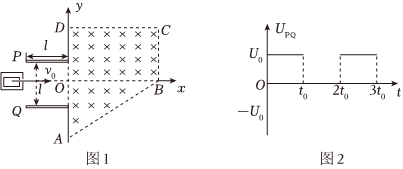 發布:2024/12/30 0:0:1組卷:89引用:2難度:0.7
發布:2024/12/30 0:0:1組卷:89引用:2難度:0.7 -
 2.如圖,半徑為d的圓形區域內有磁感應強度為B的勻強磁場,磁場垂直圓所在的平面。一帶電量為q、質量為m的帶電粒子從圓周上a點對準圓心O射入磁場,從b點折射出來,若α=60°,則帶電粒子射入磁場的速度大小為( )
2.如圖,半徑為d的圓形區域內有磁感應強度為B的勻強磁場,磁場垂直圓所在的平面。一帶電量為q、質量為m的帶電粒子從圓周上a點對準圓心O射入磁場,從b點折射出來,若α=60°,則帶電粒子射入磁場的速度大小為( )A. qBdmB. √3qBdmC. 2qBdmD. 3qBdm發布:2025/1/6 0:30:5組卷:272引用:2難度:0.6 -
 3.如圖所示,三角形ABC內有垂直于三角形平面向外的勻強磁場,AB邊長為L,∠CAB=30°,∠B=90°,D是AB邊的中點。現在DB段上向磁場內射入速度大小相同、方向平行于BC的同種粒子(不考慮粒子間的相互作用和粒子重力),若從D點射入的粒子恰好能垂直AC邊射出磁場,則AC邊上有粒子射出的區域長度為( )
3.如圖所示,三角形ABC內有垂直于三角形平面向外的勻強磁場,AB邊長為L,∠CAB=30°,∠B=90°,D是AB邊的中點。現在DB段上向磁場內射入速度大小相同、方向平行于BC的同種粒子(不考慮粒子間的相互作用和粒子重力),若從D點射入的粒子恰好能垂直AC邊射出磁場,則AC邊上有粒子射出的區域長度為( )A. L14B. L13C. L√3-12D. L√3-13發布:2025/1/3 0:30:3組卷:303引用:1難度:0.5


